Question

设0＜a＜1，则函数f（x）=log_a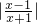

1. A.
   在（-∞，-1）上单调递减，在（-1，1）上单调递增
2. B.
   在（-∞，-1）上单调递增，在（-1，1）上单调递减
3. C.
   在（-∞，-1）上单调递增，在（-1，1）上单调递增
4. D.
   在（-∞，-1）上单调递减，在（-1，1）上单调递减

Answer 1

A
分析：求出函数f（x）的定义域，先判断x＜-1及-1＜x＜1时t=||的单调性，再根据y=log_at单调递减及复合函数单调性的判定方法可知f（x）的单调性．
解答：函数f（x）的定义域为{x|x≠±1}，
当x＜-1时，t=||==1-，单调递增，
而0＜a＜1，所以y=log_at单调递减，
所以f（x）在（-∞，-1）上单调递减；
当-1＜x＜1时，t=||=-=-1+，单调递减，
而0＜a＜1，所以y=log_at单调递减，
所以f（x）在（-1，1）上单调递增，
故选A．
点评：本题考查对数函数单调性及复合函数单调性的判定，熟记基本函数的单调性为解决该类题目提供了简捷方法．