题目内容
袋中有大小相同的4个红球与2个白球.
(1)若从袋中依次不放回取出一个球,求第三次取出白球的概率;
(2)若从袋中依次不放回取出一个球,求第一次取出红球的条件下第三次仍取出红球的概率.
(3)若从中有放回的依次取出一个球,记6次取球中取出红球的次数为ξ,求P(ξ≤4)与E(9ξ-1).
解:(1)从袋中依次不放回取出一个球取三次共有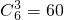 种情况,第三次取出白球共有
种情况,第三次取出白球共有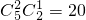 种情况
种情况
∴从袋中依次不放回取出一个球,第三次取出白球的概率为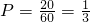 ;
;
(2)第一次取出红球后,还剩下3红2白,共5个球,故第一次取出红球的条件下第三次仍取出红球的概率为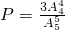 =
= ;
;
(3)记取一次球取出红球为事件A,则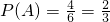 ,ξ服从二项分布,即ξ~B(6,
,ξ服从二项分布,即ξ~B(6, )
)
∴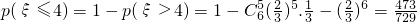
∵Eξ=6× =4
=4
∴E(9ξ-1)=9Eξ-1=9×4-1=35
分析:(1)求出从袋中依次不放回取出一个球取三次的所有可能,第三次取出白球的可能情况,即可求得从袋中依次不放回取出一个球,第三次取出白球的概率;
(2)第一次取出红球后,还剩下3红2白,共5个球,故可求第一次取出红球的条件下第三次仍取出红球的概率;
(3)记取一次球取出红球为事件A,则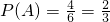 ,ξ服从二项分布,即ξ~B(6,
,ξ服从二项分布,即ξ~B(6, ),利用对立事件可求P(ξ≤4),利用Eξ=6×
),利用对立事件可求P(ξ≤4),利用Eξ=6× =4,即可求得E(9ξ-1).
=4,即可求得E(9ξ-1).
点评:本题考查概率轭求解,考查条件概率,考查数学期望,解题的关键是正确运用概率模型,合理运用二项分布的期望公式.
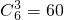 种情况,第三次取出白球共有
种情况,第三次取出白球共有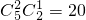 种情况
种情况∴从袋中依次不放回取出一个球,第三次取出白球的概率为
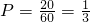 ;
;(2)第一次取出红球后,还剩下3红2白,共5个球,故第一次取出红球的条件下第三次仍取出红球的概率为
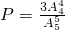 =
= ;
;(3)记取一次球取出红球为事件A,则
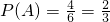 ,ξ服从二项分布,即ξ~B(6,
,ξ服从二项分布,即ξ~B(6, )
)∴
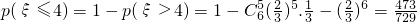
∵Eξ=6×
 =4
=4∴E(9ξ-1)=9Eξ-1=9×4-1=35
分析:(1)求出从袋中依次不放回取出一个球取三次的所有可能,第三次取出白球的可能情况,即可求得从袋中依次不放回取出一个球,第三次取出白球的概率;
(2)第一次取出红球后,还剩下3红2白,共5个球,故可求第一次取出红球的条件下第三次仍取出红球的概率;
(3)记取一次球取出红球为事件A,则
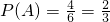 ,ξ服从二项分布,即ξ~B(6,
,ξ服从二项分布,即ξ~B(6, ),利用对立事件可求P(ξ≤4),利用Eξ=6×
),利用对立事件可求P(ξ≤4),利用Eξ=6× =4,即可求得E(9ξ-1).
=4,即可求得E(9ξ-1).点评:本题考查概率轭求解,考查条件概率,考查数学期望,解题的关键是正确运用概率模型,合理运用二项分布的期望公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 同的4个红球与2个白球。
同的4个红球与2个白球。 2)若从袋中依次不放回取出
2)若从袋中依次不放回取出 ,求
,求 与
与
 ,求
,求 与
与
 分别表示取得的红球数与白球数,计算
分别表示取得的红球数与白球数,计算 、
、 、
、 、
、 .
.