题目内容
已知各项均不相同的等差数列{an}的前四项和Sn=14,且a1,a3,a7成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列{
}的前n项和,求T2012的值.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列{
| 1 | an•an+1 |
分析:(Ⅰ)设公差为d,由Sn=14,且a1,a3,a7成等比数列,得
,由此能求出数列{an}的通项公式.
(Ⅱ)由an=n+1,知
=
=
-
,由此能求出T2012的值.
|
(Ⅱ)由an=n+1,知
| 1 |
| anan+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
解答:解:(Ⅰ)设公差为d,
∵Sn=14,且a1,a3,a7成等比数列,
∴
,…(4分)
解得d=0(舍)或d=1,所以a1=2,
故an=n+1.…(7分)
(Ⅱ)∵an=n+1,
∴
=
=
-
,
所以Tn=
-
+
-
+…+
-
=
-
,…(12分)
所以T2012=
.…(14分)
∵Sn=14,且a1,a3,a7成等比数列,
∴
|
解得d=0(舍)或d=1,所以a1=2,
故an=n+1.…(7分)
(Ⅱ)∵an=n+1,
∴
| 1 |
| anan+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
所以Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
所以T2012=
| 503 |
| 1007 |
点评:本题考查数列的通项公式和数列的前n项和的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
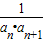 }的前n项和,求T2012的值.
}的前n项和,求T2012的值.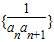 的前n项和,求T2013的值.
的前n项和,求T2013的值.