题目内容
已知中心在原点,焦点在x轴上的双曲线的离心率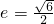 ,其焦点到渐近线的距离为1,则此双曲线的方程为
,其焦点到渐近线的距离为1,则此双曲线的方程为
- A.
 -y2=1
-y2=1 - B.
 -
- =1
=1 - C.

 -y2=1
-y2=1 - D.x2-y2=1
A
分析:设出双曲线方程,利用双曲线的离心率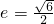 ,其焦点到渐近线的距离为1,建立方程,即可求得双曲线的方程.
,其焦点到渐近线的距离为1,建立方程,即可求得双曲线的方程.
解答:设双曲线的方程为 ,渐近线方程为
,渐近线方程为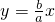
∵双曲线的离心率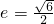 ,其焦点到渐近线的距离为1,
,其焦点到渐近线的距离为1,
∴ ,
,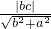 =1
=1
∴b=1,a=
∴双曲线的方程为 -y2=1
-y2=1
故选A.
点评:本题考查双曲线的标准方程,考查双曲线的几何性质,属于中档题.
分析:设出双曲线方程,利用双曲线的离心率
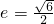 ,其焦点到渐近线的距离为1,建立方程,即可求得双曲线的方程.
,其焦点到渐近线的距离为1,建立方程,即可求得双曲线的方程.解答:设双曲线的方程为
 ,渐近线方程为
,渐近线方程为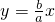
∵双曲线的离心率
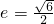 ,其焦点到渐近线的距离为1,
,其焦点到渐近线的距离为1,∴
 ,
,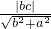 =1
=1∴b=1,a=

∴双曲线的方程为
 -y2=1
-y2=1故选A.
点评:本题考查双曲线的标准方程,考查双曲线的几何性质,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目