题目内容
2.设F是抛物线C:y2=4x的焦点,过F的直线l交抛物线C于A,B两点,当|AB|=8时,以AB为直径的圆与y轴相交所得弦长是2$\sqrt{7}$.分析 求得抛物线的焦点F,设出直线AB的方程,代入抛物线方程,运用韦达定理和中点坐标公式,再由弦长公式求得斜率,再由圆的弦长公式,可得所求值.
解答 解:y2=4x的焦点F(1,0),设直线AB:y=k(x-1),
代入抛物线的方程可得,k2x2-(2k2+4)x+k2=0,
设A(x1,y1),B(x2,y2),
即有x1+x2=2+$\frac{4}{{k}^{2}}$,即有中点的横坐标为1+$\frac{2}{{k}^{2}}$,
由抛物线的弦长公式可得,|AB|=x1+x2+p=2+$\frac{4}{{k}^{2}}$+2=8,
解得k=±1,
即有r=4,d=1+$\frac{2}{{k}^{2}}$=3,
再由圆的弦长公式可得,
与y轴相交所得弦长是2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{{4}^{2}-{3}^{2}}$=2$\sqrt{7}$.
故答案为:2$\sqrt{7}$.
点评 本题考查抛物线的方程和性质,主要是弦长公式的运用,同时考查圆的弦长公式,属于中档题.

练习册系列答案
相关题目
10.已知离散型随机变量ξ的概率分布为
则P(ξ=2)=0.52.
| ξ | 0 | 1 | 2 | 3 |
| P | 0.12 | 0.24 | 0.12 |
7. 如图,某电路在A、B之间有四个焊接点,现已知一个焊点脱落导致电路不通,则焊点脱落的不同情况有( )
如图,某电路在A、B之间有四个焊接点,现已知一个焊点脱落导致电路不通,则焊点脱落的不同情况有( )
 如图,某电路在A、B之间有四个焊接点,现已知一个焊点脱落导致电路不通,则焊点脱落的不同情况有( )
如图,某电路在A、B之间有四个焊接点,现已知一个焊点脱落导致电路不通,则焊点脱落的不同情况有( )| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
14.已知P(x,y)是中心在原点,焦距为4$\sqrt{2}$的双曲线上一点,且$\frac{y}{x}$的取值范围为(-1,1),则该双曲线的方程是( )
| A. | x2-y2=8 | B. | y2-x2=8 | C. | x2-y2=4 | D. | y2-x2=4 |
11.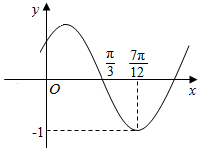 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为( )
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为( )
 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为( )
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为( )| A. | y=sin2x | B. | y=sin(2x+$\frac{π}{3}$) | C. | y=sin(2x+$\frac{π}{6}$) | D. | y=sin(2x-$\frac{π}{3}$) |
12.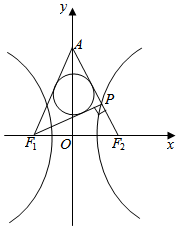 如图,F1,F2为双曲线C的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为( )
如图,F1,F2为双曲线C的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为( )
 如图,F1,F2为双曲线C的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为( )
如图,F1,F2为双曲线C的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |