题目内容
设等差数列{an}的各项均为整数,其公差d≠0,a5=6.
(Ⅰ)若a2•a10>0,求d的值;
(Ⅱ)若a3=2,且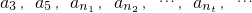 (5<n1<n2<…<nt<…)成等比数列,求nt;
(5<n1<n2<…<nt<…)成等比数列,求nt;
(Ⅲ)若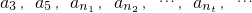 (5<n1<n2<…<nt<…)成等比数列,求n1的取值集合.
(5<n1<n2<…<nt<…)成等比数列,求n1的取值集合.
(Ⅰ)解:因为等差数列{an}的各项均为整数,所以d∈Z.(1分)
由a2•a10>0,得(a5-3d)(a5+5d)>0,即(3d-6)(5d+6)<0,解得 .
.
注意到d∈Z,且d≠0,所以d=-1,或d=1.(3分)
(Ⅱ)解:由a3=2,a5=6,得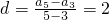 ,
,
从而an=a3+(n-3)d=2+(n-3)×2=2n-4,故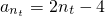 .(5分)
.(5分)
由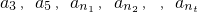 ,成等比数列,得此等比数列的公比为
,成等比数列,得此等比数列的公比为 ,
,
从而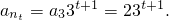
由2nt-4=2•3t+1,解得nt=3t+1+2,t=1,2,3,.(7分)
(Ⅲ)解:由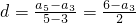 ,得
,得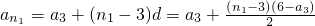 .
.
由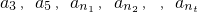 ,成等比数列,得
,成等比数列,得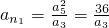 .
.
由 ,化简整理得
,化简整理得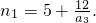 (9分)
(9分)
因为n1>5,从而a3>0,
又n1∈Z且d≠0,从而a3是12的非6的正约数,故a3=1,2,3,4,12.(10分)
①当a3=1或a3=3时,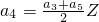 ,
,
这与{an}的各项均为整数相矛盾,所以,a3≠1且a3≠3.(11分)
②当a3=4时,由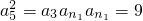 ,
,
但此时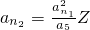 ,这与{an}的各项均为整数相矛盾,所以,a3≠4.(12分)
,这与{an}的各项均为整数相矛盾,所以,a3≠4.(12分)
③当a3=12时,同理可检验an2∉Z,所以,a3≠12.(13分)
当a3=2时,由(Ⅱ)知符合题意.
综上,n1的取值只能是n1=11,即n1的取值集合是{11}.(14分)
分析:(I)要求d,则用“a5,d”表示a2•a10>0,再由各项均为整数从而求得d;
(II)因为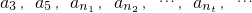 成等比数列且知道首项,故先求出公比,再用通项公式求解;
成等比数列且知道首项,故先求出公比,再用通项公式求解;
(III)与(II)思路相同,区别在于过程中用a3表示.
点评:本题主要考查等差、等比数列的概念以及分类讨论的思想.
由a2•a10>0,得(a5-3d)(a5+5d)>0,即(3d-6)(5d+6)<0,解得
 .
.注意到d∈Z,且d≠0,所以d=-1,或d=1.(3分)
(Ⅱ)解:由a3=2,a5=6,得
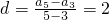 ,
,从而an=a3+(n-3)d=2+(n-3)×2=2n-4,故
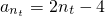 .(5分)
.(5分)由
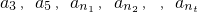 ,成等比数列,得此等比数列的公比为
,成等比数列,得此等比数列的公比为 ,
,从而
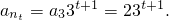
由2nt-4=2•3t+1,解得nt=3t+1+2,t=1,2,3,.(7分)
(Ⅲ)解:由
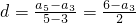 ,得
,得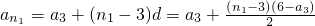 .
.由
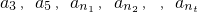 ,成等比数列,得
,成等比数列,得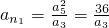 .
.由
 ,化简整理得
,化简整理得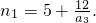 (9分)
(9分)因为n1>5,从而a3>0,
又n1∈Z且d≠0,从而a3是12的非6的正约数,故a3=1,2,3,4,12.(10分)
①当a3=1或a3=3时,
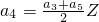 ,
,这与{an}的各项均为整数相矛盾,所以,a3≠1且a3≠3.(11分)
②当a3=4时,由
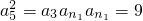 ,
,但此时
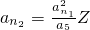 ,这与{an}的各项均为整数相矛盾,所以,a3≠4.(12分)
,这与{an}的各项均为整数相矛盾,所以,a3≠4.(12分)③当a3=12时,同理可检验an2∉Z,所以,a3≠12.(13分)
当a3=2时,由(Ⅱ)知符合题意.
综上,n1的取值只能是n1=11,即n1的取值集合是{11}.(14分)
分析:(I)要求d,则用“a5,d”表示a2•a10>0,再由各项均为整数从而求得d;
(II)因为
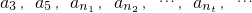 成等比数列且知道首项,故先求出公比,再用通项公式求解;
成等比数列且知道首项,故先求出公比,再用通项公式求解;(III)与(II)思路相同,区别在于过程中用a3表示.
点评:本题主要考查等差、等比数列的概念以及分类讨论的思想.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目