题目内容
已知全集为R,A={y|a<y<a2+1},B={y|y=
x2-x+
,0<x≤3}
(1)若a=2,求(CRA)∩B;
(2)若A∩B=∅,求a的取值范围.
| 1 |
| 2 |
| 5 |
| 2 |
(1)若a=2,求(CRA)∩B;
(2)若A∩B=∅,求a的取值范围.
分析:(1)当a=2时,A={y|2<y<5},CRA={y|y≥5或y≤2},B={y|y=
x2-x+
,0<x≤3}={y|2≤y≤4},从而可求
(2)由题意可得A={y|a<y<a2+1},B={y|2≤y≤4},由A∩B=∅可得a2+1≤2或a≥2,从而可求a的范围
| 1 |
| 2 |
| 5 |
| 2 |
(2)由题意可得A={y|a<y<a2+1},B={y|2≤y≤4},由A∩B=∅可得a2+1≤2或a≥2,从而可求a的范围
解答:解:(1)当a=2时,A={y|a<y<a2+1}={y|2<y<5},CRA={y|y≥5或y≤2}
∵B={y|y=
x2-x+
,0<x≤3}
={y|y=
(x-1)2+2,0<x≤3}={y|2≤y≤4}
∴(CRA)∩B={2}
(2)∵A={y|a<y<a2+1}
B={y|y=
x2-x+
,0<x≤3}
={y|y=
(x-1)2+2,0<x≤3}={y|2≤y≤4}
又∵A∩B=∅
∴a2+1≤2或a≥2
∴-1≤a≤1或a≥2
∵B={y|y=
| 1 |
| 2 |
| 5 |
| 2 |
={y|y=
| 1 |
| 2 |
∴(CRA)∩B={2}
(2)∵A={y|a<y<a2+1}
B={y|y=
| 1 |
| 2 |
| 5 |
| 2 |
={y|y=
| 1 |
| 2 |
又∵A∩B=∅
∴a2+1≤2或a≥2
∴-1≤a≤1或a≥2
点评:本题主要考查了集合的交集、并集、补集的基本运算,二次函数在闭区间上的值域的求解,解题的关键是利用数轴.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
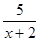 ≥1},求CR(A∩B)
≥1},求CR(A∩B)