题目内容
已知全集为R，A={x|x2-x-6≤0}，B={x|x2+2x-8＞0}，C={x|x2-4mx+3m2＜0，m＜0}．（1）求A∩B；
（2）如果（∁RA）∩（∁RB）⊆C，试求实数m的取值范围．
【答案】分析：（1）根据题意，由一元二次不等式的解法，可得集合A、B，进而由交集的意义，计算可得答案；
（2）由（1）可得集合A、B，由交集、补集的运算可得（∁RA）∩（∁RB），解x2-4mx+3m2＜0可得集合C，结合题意可得{x|-4≤x＜-2}⊆{x|3m＜x＜m，m＜0}，分析可得关于m的关系式，解可得答案．
解答：解：（1）x2-x-6≤0⇒-2≤x≤3，x2+2x-8＞0⇒x＜-4或x＞2，
则A={x|-2≤x≤3}，B={x|x＜-4或x＞2}，
得A∩B={x|2＜x≤3}．
（2）根据题意，C={x|3m＜x＜m，m＜0}，（∁RA）∩（∁RB）={x|-4≤x＜-2}，
则{x|-4≤x＜-2}⊆{x|3m＜x＜m，m＜0}，
即有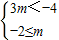
，解可得-2≤m＜-
，
则实数m的取值范围是[-2，-
）．
点评：本题考查集合的运算，涉及参数的取值问题，注意结合集合C中的条件m＜0，可得集合C．
（2）由（1）可得集合A、B，由交集、补集的运算可得（∁RA）∩（∁RB），解x2-4mx+3m2＜0可得集合C，结合题意可得{x|-4≤x＜-2}⊆{x|3m＜x＜m，m＜0}，分析可得关于m的关系式，解可得答案．
解答：解：（1）x2-x-6≤0⇒-2≤x≤3，x2+2x-8＞0⇒x＜-4或x＞2，
则A={x|-2≤x≤3}，B={x|x＜-4或x＞2}，
得A∩B={x|2＜x≤3}．
（2）根据题意，C={x|3m＜x＜m，m＜0}，（∁RA）∩（∁RB）={x|-4≤x＜-2}，
则{x|-4≤x＜-2}⊆{x|3m＜x＜m，m＜0}，
即有
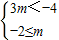，解可得-2≤m＜-，则实数m的取值范围是[-2，-
）．点评：本题考查集合的运算，涉及参数的取值问题，注意结合集合C中的条件m＜0，可得集合C．
练习册系列答案
相关题目
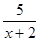≥1}，求CR（A∩B）