题目内容

设数列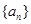的前n项和为，

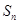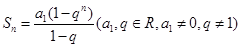
（1）求证：数列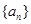是等比数列；

（2）若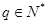，是否存在q的某些取值，使数列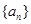中某一项能表示为另外三项之和？若能求出q的全部取值集合，若不能说明理由。

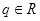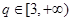（3）若，是否存在，使数列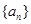中，某一项可以表示为另外三项之和？若存在指出q的一个取值，若不存在，说明理由。

 

【答案】

解：（1）n=1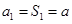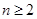时，，                   

时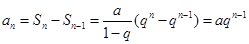，（n=1也符合） 

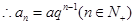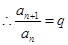，，即数列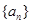是等比数列。   

（2）若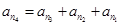则  

可设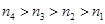，两边同除以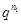得：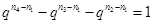

因为左边能被q整除，右边不能被q整除，因此满足条件的q不存在。

（3）若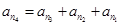则  

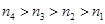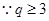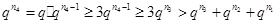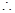
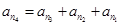可设，，，不成立。

【解析】略

 

练习册系列答案
相关题目
已知公差不为0的等差数列{an}的首项a1为a（a∈R）设数列的前n项和为Sn，且
1
a1
，
1
a2
，
1
a4
成等比数列．
（Ⅰ）求数列{an}的通项公式及Sn；
（Ⅱ）记An=
1
S1
+
1
S2
+
1
S3
+…+
1
Sn
，Bn=
1
a1
+
1
a2
+…+
1
a2n-1
，当n≥2时，试比较An与Bn的大小．
已知等差数列{an}的首项为a（a∈R，a≠0）．设数列的前n项和为Sn，且对任意正整数n都有
a2n
an
=
4n-1
2n-1
．
（1）求数列{an}的通项公式及Sn；
（2）是否存在正整数n和k，使得Sn，Sn+1，Sn+k成等比数列？若存在，求出n和k的值；若不存在，请说明理由．
已知公差不为0的等差数列{an}的首项为4，设数列的前n项和为Sn，且
1
a1
，
1
a2
，
1
a4
成等比数列．
（1）求数列{an}的通项公式an及Sn；
（2）记An=
1
S1
+
1
S2
+
1
S3
+…+
1
Sn
，Bn=
1
a1
+
1
a2
+
1
a22
+…+
1
a2n-1
，当n≥2时，试比较An与Bn的大小．
已知公差不为0的等差数列{an}的首项a1=a，a∈N*，设数列的前n项和为Sn，且
1
a1
，
1
a2
，
1
a4
成等比数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设An=
1
S1
+
1
S2
+
1
S3
+…+
1
Sn
，若A2011=
2011
2012
，求a的值．

（本小题满分12分）设数列的前n项和为Sn=2n2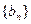，为等比数列，且（Ⅰ）求数列和的通项公式；
（Ⅱ）设，求数列的前n项和Tn.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网