题目内容
已知不等式x2-5mx-6m2≤0的解集为A,不等式ax2-x+12a-2<0的解集为B,
(1)求A;
(2)当m=1时,A∩B≠∅,求实数a的取值范围.
(1)求A;
(2)当m=1时,A∩B≠∅,求实数a的取值范围.
(1)原不等式变形为:(x+m)(x-6m)≤0,
当m>0时,A=[-m,6m];当m=0时,A={0};当m<0时,A=[6m,-m];…(5分)
(2)当m=1时,A=[-1,6];∵A∩B≠∅,
即x∈[-1,6]时,不等式ax2-x+12a-2<0有解,…(7分)
即(x2+12)a<x+2有解,也就是a<
有解,则a<(
)max…(9分)
令t=x+2,∵x∈[-1,6],∴t∈[1,8],且x=t-2
∴
=
=
=
≤
=
,
(当且仅当,即t=4时取等号),∴(
)min=
,则a<
,
故实数a的取值范围是(-∞,
)…(13分)
当m>0时,A=[-m,6m];当m=0时,A={0};当m<0时,A=[6m,-m];…(5分)
(2)当m=1时,A=[-1,6];∵A∩B≠∅,
即x∈[-1,6]时,不等式ax2-x+12a-2<0有解,…(7分)
即(x2+12)a<x+2有解,也就是a<
| x+2 |
| x2+12 |
| x+2 |
| x2+12 |
令t=x+2,∵x∈[-1,6],∴t∈[1,8],且x=t-2
∴
| x+2 |
| x2+12 |
| t |
| (t-2)2+12 |
| t |
| t2-4t+16 |
| 1 | ||
t+
|
| 1 | ||||
2
|
| 1 |
| 4 |
(当且仅当,即t=4时取等号),∴(
| x+2 |
| x2+12 |
| 1 |
| 4 |
| 1 |
| 4 |
故实数a的取值范围是(-∞,
| 1 |
| 4 |

练习册系列答案
相关题目
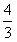 )x+6在(-∞,+∞)上有极值;求使P正确且Q正确的m的取值范围。
)x+6在(-∞,+∞)上有极值;求使P正确且Q正确的m的取值范围。 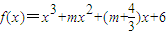 在(-∞,+∞)上有极值.求使P正确且Q正确的m的取值范围.
在(-∞,+∞)上有极值.求使P正确且Q正确的m的取值范围.