题目内容
已知m∈R,设P:x1和x2是方程x2-ax-2=0的两个实根,不等式|m2-5m-3|≥|x1-x2|的任意实数a∈[-1,1]恒成立;Q:函数f(x)=x3+mx2+(m+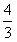 )x+6在(-∞,+∞)上有极值;求使P正确且Q正确的m的取值范围。
)x+6在(-∞,+∞)上有极值;求使P正确且Q正确的m的取值范围。
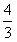 )x+6在(-∞,+∞)上有极值;求使P正确且Q正确的m的取值范围。
)x+6在(-∞,+∞)上有极值;求使P正确且Q正确的m的取值范围。 解:(1)由题设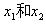 是方程
是方程 的两个实根,
的两个实根,
得 ,
,
所以,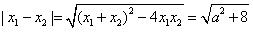 ,
,
当a∈[-1,1]时,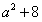 的最大值为9,即
的最大值为9,即 ;
;
由题意,不等式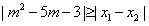 对任意实数a∈[-1,1]恒成立的m的解集
对任意实数a∈[-1,1]恒成立的m的解集
等于不等式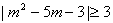 的解集,
的解集,
由此不等式得
不等式①的解为 ,不等式②的解为
,不等式②的解为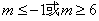 ,
,
因此,当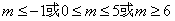 时,P是正确的;
时,P是正确的;
(2)对函数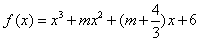 求导
求导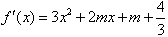 ,
,
令f′(x)=0,即 ,
,
此一元二次方程的判别式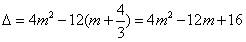 ,
,
若△=0,则f′(x)=0有两个相等的实根x0,且f′(x)的符号如下:
因此,f(x0)不是函数f(x)的极值;
若△>0,则f′(x)=0有两个不相等的实根 的符号如下:
的符号如下:
因此,函数f(x)在x=x1处取得极大值,在x=x2处取得极小值;
综上所述,当且仅当△>0时,f(x)在(-∞,+∞)上有极值,
由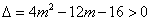 得m<-1或m>4,
得m<-1或m>4,
因此,当m<-1或m>4时,Q是正确的;
综上,使P正确且Q正确时,实数m的取值范围为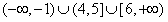 。
。

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 有两个不同的零点.求使“P且Q”为真命题的实数m的取值范围.
有两个不同的零点.求使“P且Q”为真命题的实数m的取值范围.