题目内容

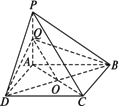
如图所示，P是平行四边形ABCD所在平面外一点，Q是PA的中点，求证：PC∥平面BDQ．

答案：
解析：

　　证明：连结AC交BD于O．

　　∵四边形ABCD是平行四边形，

　　∴AO＝OC．连结OQ，

　　又OQ是△APC的中位线，∴PC∥OQ．

　　∵PC在平面BDQ外，OQ平面BDQ，

　　∴PC∥平面BDQ．


练习册系列答案
相关题目
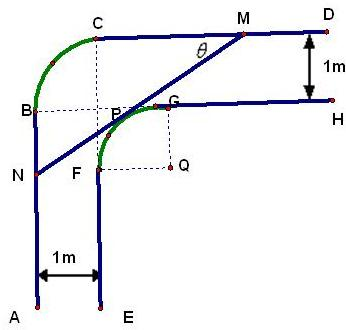精英家教网一走廊拐角下的横截面如图所示，已知内壁FG和外壁BC都是半径为1m的四分之一圆弧，AB，DC分别与圆弧BC相切于B、C两点，EF∥AB，GH∥CD，且两组平行墙壁间的走廊宽度都是1m．
（1）若水平放置的木棒MN的两个端点M、N分别在外壁CD和AB上，且木棒与内壁圆弧相切于点P．设∠CMN=θ（rad），试用θ表示木棒MN和长度f（θ）．
（2）若一根水平放置的木棒能通过该走廊拐角处，求木棒长度的最大值．
如图所示，四棱锥P-ABCD中，底面ABCD是直角梯形，∠DAB=∠ABC=90°，若PA⊥平面ABCD，且左视图投影平面与平面PAB平行，则下列选项中可能是四棱锥P-ABCD左视图的是（　　）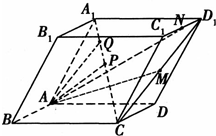
如图所示，在各个面都是平行四边形的四棱柱ABCD-A1B1C1D1中，P是CA1的中点，M是CD1的中点，N是C1D1的中点，点Q在CA1上，且CQ：QA1=4：1，设
AB
=a，
AD
=b，
AA1
=c，用基底{a，b，c}表示以下向量：
（1）
AP
；
（2）
AM
；
（3）
AN
；
（4）
AQ
．
（2009•黄浦区二模）已知四棱锥P-ABCD的底面是∠BAD=60°的菱形，如图所示，则该四棱锥的主视图（AB平行于主视图的投影平面）可能是（　　）

一走廊拐角处的横截面如图所示，已知内壁FG和外壁BC都是半径为1m的四分之一圆弧，AB、DC分别与圆弧BC相切于点B、C两点，，且两组平行墙壁间的走廊宽度都是1m，

（1）若水平放置的木棒MN的两个端点M、N分别在外壁CD和AB上，且木棒与内壁圆弧相切于点P，设，试用表示木棒MN的长度；

（2）若一根水平放置的木棒能通过该走廊拐角处，则求木棒长度的最大值。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网