题目内容
已知函数f(x)=x3+mx2+nx+m-1,当x=-1时取得极值,且函数y=f(x)在点(1,f(1))处的切线的斜率为4.
(Ⅰ)求f(x)的解析式;
(Ⅱ)O是坐标原点,A点是x轴上横坐标为2的点,B点是曲线 上但不在x轴上的动点,求△AOB面积的最大值.
上但不在x轴上的动点,求△AOB面积的最大值.
解:(Ⅰ)由已知得f′(x)=3x2+2mx+n…(1分)
由已知得 ,∴
,∴ .
.
故f(x)=x3+x2-x…(5分)
(Ⅱ)由(Ⅰ)得f′(x)=3x2+2x-1=(x+1)(3x-1)
∴f(x)在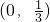 上为减函数,在
上为减函数,在 上为增函数 …(7分)
上为增函数 …(7分)
要使△OAB的面积最大,由O、A两点在x轴上且|OA|=2知,只需在 上,|f(xB)|的值最大,
上,|f(xB)|的值最大,
由f(x)在区间 上的单调性知,只有当
上的单调性知,只有当 或
或 时,|f(xB)|的值最大…(9分)
时,|f(xB)|的值最大…(9分)
而 …(10分)
…(10分)
故当 时,△OAB的面积最大,且最大值为
时,△OAB的面积最大,且最大值为 …(12分)
…(12分)
分析:(Ⅰ)求导函数,利用函数y=f(x)在点(1,f(1))处的切线的斜率为4,建立方程组,可得f(x)的解析式;
(Ⅱ)求导数,确定函数的单调性,要使△OAB的面积最大,由O、A两点在x轴上且|OA|=2知,只需在 上,|f(xB)|的值最大,由此可求△AOB面积的最大值.
上,|f(xB)|的值最大,由此可求△AOB面积的最大值.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,解题的关键是正确求导数.
由已知得
 ,∴
,∴ .
.故f(x)=x3+x2-x…(5分)
(Ⅱ)由(Ⅰ)得f′(x)=3x2+2x-1=(x+1)(3x-1)
∴f(x)在
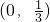 上为减函数,在
上为减函数,在 上为增函数 …(7分)
上为增函数 …(7分)要使△OAB的面积最大,由O、A两点在x轴上且|OA|=2知,只需在
 上,|f(xB)|的值最大,
上,|f(xB)|的值最大,由f(x)在区间
 上的单调性知,只有当
上的单调性知,只有当 或
或 时,|f(xB)|的值最大…(9分)
时,|f(xB)|的值最大…(9分)而
 …(10分)
…(10分)故当
 时,△OAB的面积最大,且最大值为
时,△OAB的面积最大,且最大值为 …(12分)
…(12分)分析:(Ⅰ)求导函数,利用函数y=f(x)在点(1,f(1))处的切线的斜率为4,建立方程组,可得f(x)的解析式;
(Ⅱ)求导数,确定函数的单调性,要使△OAB的面积最大,由O、A两点在x轴上且|OA|=2知,只需在
 上,|f(xB)|的值最大,由此可求△AOB面积的最大值.
上,|f(xB)|的值最大,由此可求△AOB面积的最大值.点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,解题的关键是正确求导数.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|