Question

（理）已知点A（1，0），B（0，1）和互不相同的点P₁，P₂，P₃，…，P_n，…，满足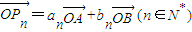，O为坐标原点，其中{a_n}、{b_n}分别为等差数列和等比数列，P₁是线段AB的中点，对于给定的公差不为零的a_n，都能找到唯一的一个b_n，使得P₁，P₂，P₃，…，P_n，…，都在一个指数函数    （写出函数的解析式）的图象上．

Answer 1

【答案】分析：设数列{a_n}的公差为d，{b_n}的公比为q，因为P₁，P₂，P₃，…P_n，是互不相同的点．由题意可得P_n（a_n，b_n），又P₁是AB中点，所以．所以．所以猜想是一个指数函数，即为f（x）=a^x，代入整理可得即a=．进而得到答案．
解答：解：设数列{a_n}的公差为d，{b_n}的公比为q，因为P₁，P₂，P₃，…P_n，是互不相同的点．
由题意可得，得P_n（a_n，b_n），又P₁是AB中点，
所以，即．
所以，
所以．
所以猜想是一个指数函数，即为f（x）=a^x，
所以===
所以即a=．
故答案为：．
点评：本题主要考查知识间的渗透问题，是向量形式和坐标形式的相互转化，点的横纵坐标是一个数列进而利用数列知识研究其关系．