题目内容
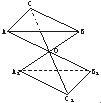如图，设△ABC和△A1B1C1的三对对应顶点的连线AA1、BB1、CC1相交于一点O，且| AO |
| OA1 |
| BO |
| OB1 |
| CO |
| OC1 |
| 2 |
| 3 |
| S△ABC |
| S△A1B1C1 |
分析：依据对应边成比例得三角形相似，由相似三角形面积的比等于相似比的平方，即可求解．
解答：解：依题意，因为AA1、BB1、CC1相交于一点O，且
=
=
，
所以AB∥A1B1，AC∥A1C1，BC∥B1C1．
由平行角定理得∠BAC=∠B1A1C1，∠ABC=∠A1B1C1，
∴△ABC∽△A1B1C1，
所以
=（
）2=
．
| AO |
| OA1 |
| BO |
| OB1 |
| CO |
| OC1 |
所以AB∥A1B1，AC∥A1C1，BC∥B1C1．
由平行角定理得∠BAC=∠B1A1C1，∠ABC=∠A1B1C1，
∴△ABC∽△A1B1C1，
所以
| S△ABC |
| S△A1B1C1 |
| 2 |
| 3 |
| 4 |
| 9 |
点评：本题主要是考查对于相似三角形面积的比等于相似比的平方的性质的掌握．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
如图，P-ABC是底面边长为1的正三棱锥，D、E、F分别为棱长PA、PB、PC上的点，截面DEF∥底面ABC，且棱台DEF-ABC与棱锥P-ABC的棱长和相等．（棱长和是指多面体中所有棱的长度之和）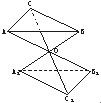
=
=
=
．试求
的值．