题目内容
设椭圆C: 的离心率为
的离心率为 ,右焦点到右准线的距离为3.
,右焦点到右准线的距离为3.
(1)求椭圆C的方程;
(2)过E( ,0)作倾角为锐角的直线l交椭圆于A,B两点,若
,0)作倾角为锐角的直线l交椭圆于A,B两点,若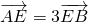 ,求l的方程.
,求l的方程.
解:(1)∵椭圆C: 的离心率为
的离心率为 ,右焦点到右准线的距离为3
,右焦点到右准线的距离为3
∴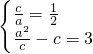 ,∴c=1,a=2
,∴c=1,a=2
∴b2=a2-c2=3
∴椭圆C的方程为 ;
;
(2)设l:x=λy+ (λ>0),代入椭圆方程,消去x可得(3λ2+4)y2+9λy-
(λ>0),代入椭圆方程,消去x可得(3λ2+4)y2+9λy- =0
=0
设A(x1,y1)、B(x2,y2),则y1+y2= ,y1y2=
,y1y2=
∵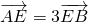 ,∴y1=-3y2,
,∴y1=-3y2,
∴ =-
=- (
( )2
)2
∴
∵λ>0,∴
∴l的方程为: .
.
分析:(1)利用椭圆C: 的离心率为
的离心率为 ,右焦点到右准线的距离为3,建立方程组,求出几何量,即可求得椭圆C的方程;
,右焦点到右准线的距离为3,建立方程组,求出几何量,即可求得椭圆C的方程;
(2)设l的方程代入椭圆方程,消去x可得一元二次方程,利用韦达定理及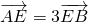 ,即可求得l的方程.
,即可求得l的方程.
点评:本题考查椭圆的标准方程与几何性质,考查直线与椭圆的位置关系,考查向量知识的运用,正确运用韦达定理是关键.
 的离心率为
的离心率为 ,右焦点到右准线的距离为3
,右焦点到右准线的距离为3∴
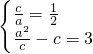 ,∴c=1,a=2
,∴c=1,a=2∴b2=a2-c2=3
∴椭圆C的方程为
 ;
;(2)设l:x=λy+
 (λ>0),代入椭圆方程,消去x可得(3λ2+4)y2+9λy-
(λ>0),代入椭圆方程,消去x可得(3λ2+4)y2+9λy- =0
=0设A(x1,y1)、B(x2,y2),则y1+y2=
 ,y1y2=
,y1y2=
∵
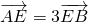 ,∴y1=-3y2,
,∴y1=-3y2,∴
 =-
=- (
( )2
)2∴

∵λ>0,∴

∴l的方程为:
 .
.分析:(1)利用椭圆C:
 的离心率为
的离心率为 ,右焦点到右准线的距离为3,建立方程组,求出几何量,即可求得椭圆C的方程;
,右焦点到右准线的距离为3,建立方程组,求出几何量,即可求得椭圆C的方程;(2)设l的方程代入椭圆方程,消去x可得一元二次方程,利用韦达定理及
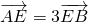 ,即可求得l的方程.
,即可求得l的方程.点评:本题考查椭圆的标准方程与几何性质,考查直线与椭圆的位置关系,考查向量知识的运用,正确运用韦达定理是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的离心率为e=
的离心率为e= ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4。
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4。 的离心率为e=
的离心率为e= ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4. ,求3x1-4y1的取值范围.
,求3x1-4y1的取值范围. 的离心率为
的离心率为 ,右焦点到右准线的距离为3.
,右焦点到右准线的距离为3. ,0)作倾角为锐角的直线l交椭圆于A,B两点,若
,0)作倾角为锐角的直线l交椭圆于A,B两点,若 ,求l的方程.
,求l的方程. 的离心率为e=
的离心率为e= ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.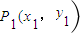 ,求3x1-4y1的取值范围.
,求3x1-4y1的取值范围.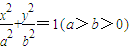 的离心率为e=
的离心率为e=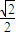 ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.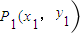 ,求3x1-4y1的取值范围.
,求3x1-4y1的取值范围.