题目内容
设椭圆C: 的离心率为e=
的离心率为e= ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.(1)求椭圆C的方程;
(2)椭圆C上一动点P(x,,y)关于直线y=2x的对称点为
 ,求3x1-4y1的取值范围.
,求3x1-4y1的取值范围.
【答案】分析:(1)依题意知,2a=4,e= 由此可求出椭圆C的方程.
由此可求出椭圆C的方程.
(2)点P(x,,y)关于直线y=2x的对称点为 ,由题设条件能推出3x1-4y1=-5x.再由点P(x,,y)在椭圆C:
,由题设条件能推出3x1-4y1=-5x.再由点P(x,,y)在椭圆C: 上,能够铁推出3x1-4y1的取值范围.
上,能够铁推出3x1-4y1的取值范围.
解答:解:(1)依题意知,2a=4,∴a=2.
∵ ,
,
∴ .
.
∴所求椭圆C的方程为 .
.
(2)∵点P(x,,y)关于直线y=2x的对称点为 ,
,
∴
解得: ,
, .
.
∴3x1-4y1=-5x.
∵点P(x,,y)在椭圆C: 上,
上,
∴-2≤x≤2,则-10≤-5x≤10.
∴3x1-4y1的取值范围为[-10,,10].
点评:本题考查椭圆的基本性质及其应用,解题时要注意公式的灵活运用.
 由此可求出椭圆C的方程.
由此可求出椭圆C的方程.(2)点P(x,,y)关于直线y=2x的对称点为
 ,由题设条件能推出3x1-4y1=-5x.再由点P(x,,y)在椭圆C:
,由题设条件能推出3x1-4y1=-5x.再由点P(x,,y)在椭圆C: 上,能够铁推出3x1-4y1的取值范围.
上,能够铁推出3x1-4y1的取值范围.解答:解:(1)依题意知,2a=4,∴a=2.
∵
 ,
,∴
 .
.∴所求椭圆C的方程为
 .
.(2)∵点P(x,,y)关于直线y=2x的对称点为
 ,
,∴

解得:
 ,
, .
.∴3x1-4y1=-5x.
∵点P(x,,y)在椭圆C:
 上,
上,∴-2≤x≤2,则-10≤-5x≤10.
∴3x1-4y1的取值范围为[-10,,10].
点评:本题考查椭圆的基本性质及其应用,解题时要注意公式的灵活运用.

练习册系列答案
相关题目
 的离心率为e=
的离心率为e= ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4。
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4。 的离心率为
的离心率为 ,右焦点到右准线的距离为3.
,右焦点到右准线的距离为3. ,0)作倾角为锐角的直线l交椭圆于A,B两点,若
,0)作倾角为锐角的直线l交椭圆于A,B两点,若 ,求l的方程.
,求l的方程. 的离心率为e=
的离心率为e= ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.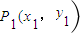 ,求3x1-4y1的取值范围.
,求3x1-4y1的取值范围.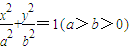 的离心率为e=
的离心率为e=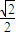 ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.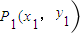 ,求3x1-4y1的取值范围.
,求3x1-4y1的取值范围.