题目内容
平面直角坐标系xOy中,双曲线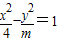 的离心率为
的离心率为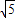 ,则m的值为 .
,则m的值为 .
【答案】分析:由双曲线方程得y2的分母m>0,所以双曲线的焦点必在x轴上.因此a2=4>0,可得c2=m+4,根据双曲线的离心率为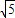 ,可得c2=5a2,建立关于m的方程,求解即可.
,可得c2=5a2,建立关于m的方程,求解即可.
解答:解:∵m>0
∴双曲线-=1的焦点必在x轴上
因此a2=4>0,b2=m
∴c2=m+4
∵双曲线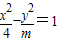 的离心率为
的离心率为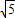 ,
,
∴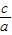 =
=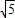 ,可得c2=5a2,
,可得c2=5a2,
所以m+4=20,解之得m=16,
故答案为:16.
点评:本题给出含有字母参数的双曲线方程,在已知离心率的情况下求参数的值,着重考查了双曲线的概念与性质,属于基础题.
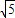 ,可得c2=5a2,建立关于m的方程,求解即可.
,可得c2=5a2,建立关于m的方程,求解即可.解答:解:∵m>0
∴双曲线-=1的焦点必在x轴上
因此a2=4>0,b2=m
∴c2=m+4
∵双曲线
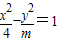 的离心率为
的离心率为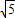 ,
,∴
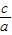 =
=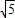 ,可得c2=5a2,
,可得c2=5a2,所以m+4=20,解之得m=16,
故答案为:16.
点评:本题给出含有字母参数的双曲线方程,在已知离心率的情况下求参数的值,着重考查了双曲线的概念与性质,属于基础题.

练习册系列答案
相关题目
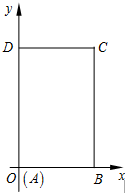 如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.
如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.