题目内容
已知向量 ,函数
,函数 .
.
(1)求函数f(x)的最大值,并写出相应x的取值集合;
(2)若 ,且α∈(0,π),求tanα的值.
,且α∈(0,π),求tanα的值.
解:(1) ,
,
所以,当 ,即当
,即当 时,f(x)max=2.
时,f(x)max=2.
所以函数f(x)的最大值为2,此时x的取值集合为:{x| }.
}.
(2)由(1)得: ,
,
由 ,可得
,可得 ,
,
从而 ,
,
由于α∈(0,π),所以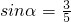 .
.
于是, .
.
分析:(1)把函数f(x)表示出来并化简,利用三角知识即可求得;
(2)先由 求出cos
求出cos ,再用倍角公式求出cosα,据平方关系求出sinα,从而可求tanα.
,再用倍角公式求出cosα,据平方关系求出sinα,从而可求tanα.
点评:本题考查平面向量的数量积运算、同角三角函数间的关系等三角知识,考查学生运算及变形能力,具有一定综合性.
 ,
,所以,当
 ,即当
,即当 时,f(x)max=2.
时,f(x)max=2.所以函数f(x)的最大值为2,此时x的取值集合为:{x|
 }.
}.(2)由(1)得:
 ,
,由
 ,可得
,可得 ,
,从而
 ,
,由于α∈(0,π),所以
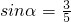 .
.于是,
 .
.分析:(1)把函数f(x)表示出来并化简,利用三角知识即可求得;
(2)先由
 求出cos
求出cos ,再用倍角公式求出cosα,据平方关系求出sinα,从而可求tanα.
,再用倍角公式求出cosα,据平方关系求出sinα,从而可求tanα.点评:本题考查平面向量的数量积运算、同角三角函数间的关系等三角知识,考查学生运算及变形能力,具有一定综合性.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 ,函数
,函数 .
. ,
, .函数
.函数 .
. 在区间
在区间 上的最大值和最小值;
上的最大值和最小值; ,若函数
,若函数 在区间(-1,1)上是增函数,则
在区间(-1,1)上是增函数,则 的取值范围为
.
的取值范围为
. ,函数
,函数 .
. 时,若f(x)=1,求x的值.
时,若f(x)=1,求x的值.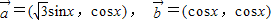 ,函数
,函数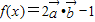 .
.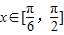 时,若f(x)=1,求x的值.
时,若f(x)=1,求x的值.