题目内容
(2012•芜湖二模)P为抛物线y2=4x上一动点,则点P到y轴距离和到点A(2,3)距离之和的最小值等于
-1
-1.
| 10 |
| 10 |
分析:先求出抛物线的准线方程,焦点坐标,由于A在抛物线的外部,所以连接焦点F和点A,AF与抛物线的交点P,即为所求点,利用抛物线的定义可求点P到y轴距离和到点A(2,3)距离之和的最小值.
解答: 解:y2=4x的准线是x=-1.抛物线的焦点坐标为(1,0)
解:y2=4x的准线是x=-1.抛物线的焦点坐标为(1,0)
由于A在抛物线的外部,所以连接焦点F和点A,AF与抛物线的交点P,即为所求点,
∵P到x=-1的距离等于P到焦点F的距离,
∴点P到y轴距离和到点A(2,3)距离之和为P到焦点F的距离
和到点A(2,3)距离之和减1,
∴当且仅当A,P,F三点共线时,点P到y轴距离和到点A(2,3)距离之和最小
∴点P到y轴距离和到点A(2,3)距离之和的最小值为|AF|-1=
-1
故答案为:
-1
 解:y2=4x的准线是x=-1.抛物线的焦点坐标为(1,0)
解:y2=4x的准线是x=-1.抛物线的焦点坐标为(1,0)由于A在抛物线的外部,所以连接焦点F和点A,AF与抛物线的交点P,即为所求点,
∵P到x=-1的距离等于P到焦点F的距离,
∴点P到y轴距离和到点A(2,3)距离之和为P到焦点F的距离
和到点A(2,3)距离之和减1,
∴当且仅当A,P,F三点共线时,点P到y轴距离和到点A(2,3)距离之和最小
∴点P到y轴距离和到点A(2,3)距离之和的最小值为|AF|-1=
| 10 |
故答案为:
| 10 |
点评:本题以抛物线的标准方程为载体,考查抛物线的定义,考查距离和,解题的关键是利用抛物线上的点到焦点的距离等于它到准线的距离.

练习册系列答案
相关题目
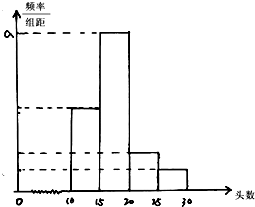 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: