题目内容
已知定点Q(0,-4)、P(6,0),动点C在椭圆
思路分析:本题为求最值问题,借助于参数方程,可以把几何的最值问题转化为三角函数的最值问题,从而可利用正弦、余弦的有界性进行求解.
解:由题设易求得PQ的方程为2x-3y-12=0,|PQ|=![]() .
.
已知椭圆的参数方程为![]() (θ为参数,且0≤θ<2π).则椭圆上点C(3cosθ,2sinθ)到直线PQ的距离d=
(θ为参数,且0≤θ<2π).则椭圆上点C(3cosθ,2sinθ)到直线PQ的距离d=
显然,当θ=![]() 时,d最大,且dmax=
时,d最大,且dmax=![]() .
.
此时S△PQC的最大值是![]() ×dmax×|PQ|=
×dmax×|PQ|=![]() ×
×![]() ×
×![]() =12+
=12+![]() ;
;
当θ=![]() 时,d最短,dmin=
时,d最短,dmin=![]() ,
,
此时S△PQC的最小值为12-![]() .
.

练习册系列答案
相关题目
 已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是
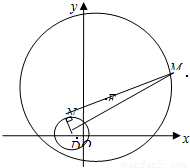
已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是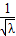 .
.
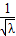 .
.