题目内容
已知a为实数,两直线l1:ax+y+1=0,l2:x+y-a=0相交于一点M,求证:交点不可能在第一象限及x轴上.
.若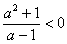 时,此点亦不在第一象限.
时,此点亦不在第一象限.
故交点不可能在第一象限内.又因为a为任意实数时,都有a2+1>0,故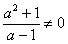 (因为a≠1,否则两直线平行,无交点).所以交点不可能在x轴上.
(因为a≠1,否则两直线平行,无交点).所以交点不可能在x轴上.
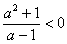 时,此点亦不在第一象限.
时,此点亦不在第一象限.故交点不可能在第一象限内.又因为a为任意实数时,都有a2+1>0,故
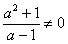 (因为a≠1,否则两直线平行,无交点).所以交点不可能在x轴上.
(因为a≠1,否则两直线平行,无交点).所以交点不可能在x轴上. 联立直线方程并解方程组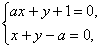
得交点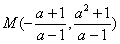 .若
.若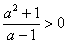 ,
,
则a>1,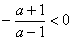 .
.
此时交点在第二象限内.若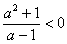 时,此点亦不在第一象限.
时,此点亦不在第一象限.
故交点不可能在第一象限内.又因为a为任意实数时,都有a2+1>0,故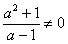 (因为a≠1,否则两直线平行,无交点).所以交点不可能在x轴上.
(因为a≠1,否则两直线平行,无交点).所以交点不可能在x轴上.
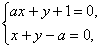
得交点
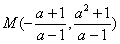 .若
.若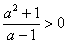 ,
,则a>1,
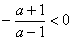 .
.此时交点在第二象限内.若
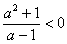 时,此点亦不在第一象限.
时,此点亦不在第一象限.故交点不可能在第一象限内.又因为a为任意实数时,都有a2+1>0,故
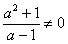 (因为a≠1,否则两直线平行,无交点).所以交点不可能在x轴上.
(因为a≠1,否则两直线平行,无交点).所以交点不可能在x轴上. 
练习册系列答案
相关题目
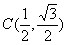 ,求△ABC的面积.
,求△ABC的面积. 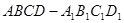 中,
中,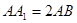 ,则异面直线
,则异面直线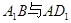 所成角的余弦值为( )
所成角的余弦值为( )

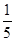
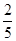
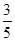
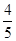
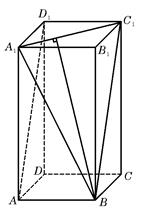
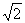
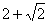
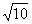
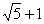
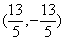
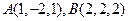 ,点
,点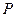 在
在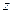 轴上,且
轴上,且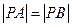 ,则点
,则点