题目内容

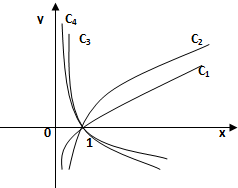如图是函数y=logax的图象，已知a值取
3
，
4
3
，
3
5
，
1
10
则相应于C1，C2，C3，C4的A值依次是（　　）
分析：令4个函数取同样的函数值1，得到的自变量的值恰好是：
1
10
、
3
5
、
4
3
、
3
，即为底数的数值，由logaa=1判断出，对应的函数y=logax的图象从左到右依次C4，C3，C2，C1．
解答：解：令4个函数的函数值为1，即1=
log
x1
1
10
，1=
log
x2
3
5
，1=
log
x3
4
3
，1=
log
x4
3
，
解得x1=
1
10
，x2=
3
5
，x3=
4
3
，x4=
3
，
∴对应的函数y=logax的图象从左到右依次C4，C3，C2，C1．
 故选A．
点评：本题主要考查了对数函数的图象的变化与对数函数的底数的联系，考查数形结合的思想．
练习册系列答案
相关题目
精英家教网某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数P与听课时间t之间的关系满足如图所示的曲线．当t∈（0，14]时，曲线是二次函数图象的一部分，当t∈[14，40]时，曲线是函数y=logα（x-5）+83（a＞0且a≠1）图象的一部分．根据专家研究，当注意力指数P大于等于80时听课效果最佳．
（1）试求P=f（t）的函数关系式；
（2）老师在什么时段内安排核心内容能使得学生听课效果最佳？
请说明理由．
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数P与听课时间t之间的关系满足如图所示的曲线．当t∈（0，14]时，曲线是二次函数图象的一部分，当t∈[14，40]时，曲线是函数y=logα（x-5）+83（a＞0且a≠1）图象的一部分．根据专家研究，当注意力指数P大于等于80时听课效果最佳．
（1）试求P=f（t）的函数关系式；
（2）老师在什么时段内安排核心内容能使得学生听课效果最佳？
请说明理由．
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数P与听课时间t之间的关系满足如图所示的曲线．当t∈（0，14]时，曲线是二次函数图象的一部分，当t∈[14，40]时，曲线是函数y=logα（x-5）+83（a＞0且a≠1）图象的一部分．根据专家研究，当注意力指数P大于等于80时听课效果最佳．
（1）试求P=f（t）的函数关系式；
（2）老师在什么时段内安排核心内容能使得学生听课效果最佳？
请说明理由．
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数P与听课时间t之间的关系满足如图所示的曲线．当t∈（0，14]时，曲线是二次函数图象的一部分，当t∈[14，40]时，曲线是函数y=logα（x-5）+83（a＞0且a≠1）图象的一部分．根据专家研究，当注意力指数P大于等于80时听课效果最佳．
（1）试求P=f（t）的函数关系式；
（2）老师在什么时段内安排核心内容能使得学生听课效果最佳？
请说明理由．
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数P与听课时间t之间的关系满足如图所示的曲线．当t∈（0，14]时，曲线是二次函数图象的一部分，当t∈[14，40]时，曲线是函数y=logα（x-5）+83（a＞0且a≠1）图象的一部分．根据专家研究，当注意力指数P大于等于80时听课效果最佳．
（1）试求P=f（t）的函数关系式；
（2）老师在什么时段内安排核心内容能使得学生听课效果最佳？
请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网