题目内容
 已知三棱柱ABC-A1B1C1的底面边长均为2,高为3,点M在线段AA1上,且AM=1,点N、P分别在线段BB1、CC1上,且NP∥BC,若平面MNP把三棱柱分成体积相等的两部分,则BN的长为
已知三棱柱ABC-A1B1C1的底面边长均为2,高为3,点M在线段AA1上,且AM=1,点N、P分别在线段BB1、CC1上,且NP∥BC,若平面MNP把三棱柱分成体积相等的两部分,则BN的长为
- A.2
- B.

- C.

- D.

C
分析:由已知三棱柱ABC-A1B1C1的底面边长均为2,高为3,我们易求出三棱柱ABC-A1B1C1的体积,又由平面MNP把三棱柱分成体积相等的两部分,则我们可以求出几何体ABC-MNP的体积,由于该几何体是一个棱柱和四棱锥组成的组合体,由此我们我们要以构造一个关于BN的方程,解方程即可求出BN的长.
解答:∵三棱柱ABC-A1B1C1的底面边长均为2,高为3,
则三棱柱ABC-A1B1C1的体积V= =
=
若平面MNP把三棱柱分成体积相等的两部分
则几何体ABC-MNP的体积VABC-MNP=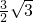
又∵VABC-MNP= +
+
∴BN=
故选C
点评:本题考查的知识点是棱柱的几何结构特征,棱柱、棱锥、棱台的体积,其中根据几何体ABC-MNP是一个棱柱和四棱锥组成的组合体,结合棱柱和棱锥体积公式构造一个关于BN的方程,是解答本题的关键.
分析:由已知三棱柱ABC-A1B1C1的底面边长均为2,高为3,我们易求出三棱柱ABC-A1B1C1的体积,又由平面MNP把三棱柱分成体积相等的两部分,则我们可以求出几何体ABC-MNP的体积,由于该几何体是一个棱柱和四棱锥组成的组合体,由此我们我们要以构造一个关于BN的方程,解方程即可求出BN的长.
解答:∵三棱柱ABC-A1B1C1的底面边长均为2,高为3,
则三棱柱ABC-A1B1C1的体积V=
 =
=
若平面MNP把三棱柱分成体积相等的两部分
则几何体ABC-MNP的体积VABC-MNP=
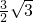
又∵VABC-MNP=
 +
+
∴BN=

故选C
点评:本题考查的知识点是棱柱的几何结构特征,棱柱、棱锥、棱台的体积,其中根据几何体ABC-MNP是一个棱柱和四棱锥组成的组合体,结合棱柱和棱锥体积公式构造一个关于BN的方程,是解答本题的关键.

练习册系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|
如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|