题目内容
有下列两个命题:
命题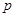 :对
:对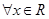 ,
, 恒成立。
恒成立。
命题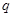 :函数
:函数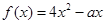 在
在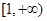 上单调递增。
上单调递增。
若“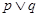 ”为真命题,“
”为真命题,“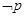 ”也为真命题,求实数
”也为真命题,求实数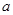 的取值范围。
的取值范围。
【答案】

【解析】
试题分析:(1)对 ,
, 恒成立,当
恒成立,当 时显然成立;
时显然成立;
当 时,必有
时,必有 ,所以命题
,所以命题
函数 在
在 上单调递增
上单调递增 ,所以命题
,所以命题
由已知: 假
假 真,所以
真,所以
考点:本题主要考查复合命题的概念,二次函数的图象和性质。
点评:典型题,涉及命题的题目,往往综合性较强。 是真命题,意味着p,q至少有一是真命题,
是真命题,意味着p,q至少有一是真命题, 是真命题,p一定是假命题。
是真命题,p一定是假命题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目