题目内容
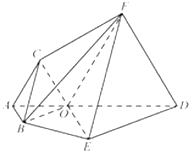 平面四边形ABED中,O在线段AD上,且OA=1,OD=2,△OAB,△ODE都是正三角形.将四边形ABED沿AD翻折后,使点B落在点C位置,点E落在点F位置,且F点在平面ABED上的射影恰为线段OD的中点(即垂线段的垂足点),所得多面体ABEDFC,如图所示
平面四边形ABED中,O在线段AD上,且OA=1,OD=2,△OAB,△ODE都是正三角形.将四边形ABED沿AD翻折后,使点B落在点C位置,点E落在点F位置,且F点在平面ABED上的射影恰为线段OD的中点(即垂线段的垂足点),所得多面体ABEDFC,如图所示(1)求棱锥F-OED的体积;
(2)证明:BC∥EF.
分析:(1)利用锥体的体积公式求解体积.
(2)利用线面平行的性质定理证明直线平行.
(2)利用线面平行的性质定理证明直线平行.
解答:解:(1)由已知可得△OAC≌△OAB,△ODE≌△ODF,
又∵OD=2,∴S△ODE=
∵F在平面ABCD的射影为线段OD的中点∴棱锥F-OED高h=
,
∴VF-OED=
S△OED•h=1
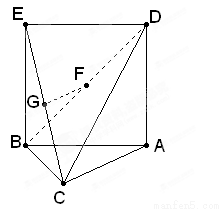
(2)设DE中点为G,DF中点为H
连结CH、BG、GH,有EF∥GH,
由已知可得,在平面ADFC中有∠COA=∠FDA=60°
∵OC∥DH
又∵OC=1,DF=2
∴DH=
DF=1
则OC∥DH,OC=DH
∴四边形ODHC为平行四边形
∴CH∥OD.CH=OD
同理可证BG∥OD,BG=OD
∴CH∥BG,CH=BG
∴四边形BCHG为平行四边形
∴BC∥GH
故BC∥EF
又∵OD=2,∴S△ODE=
| 3 |
∵F在平面ABCD的射影为线段OD的中点∴棱锥F-OED高h=
| 3 |

∴VF-OED=
| 1 |
| 3 |
(2)设DE中点为G,DF中点为H
连结CH、BG、GH,有EF∥GH,
由已知可得,在平面ADFC中有∠COA=∠FDA=60°
∵OC∥DH
又∵OC=1,DF=2
∴DH=
| 1 |
| 2 |
则OC∥DH,OC=DH
∴四边形ODHC为平行四边形
∴CH∥OD.CH=OD
同理可证BG∥OD,BG=OD
∴CH∥BG,CH=BG
∴四边形BCHG为平行四边形
∴BC∥GH
故BC∥EF
点评:本题主要考查空间几何体的体积公式以及空间直线平行的判断,要求熟练掌握相应的体积公式.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
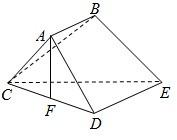 如图,多面体ABCDE中,四边形ABED是直角梯形,∠BAD=90°,DE∥AB,平面BAED^平面ACD,△ACD是边长为2a的正三角形,DE=2AB=2a,F是CD的中点
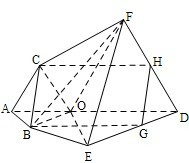
如图,多面体ABCDE中,四边形ABED是直角梯形,∠BAD=90°,DE∥AB,平面BAED^平面ACD,△ACD是边长为2a的正三角形,DE=2AB=2a,F是CD的中点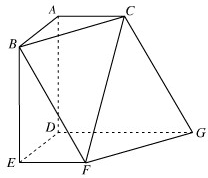 如图,多面体ABCDEFG中,AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.
如图,多面体ABCDEFG中,AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.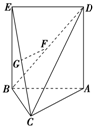 如图△ABC中,AC=BC=
如图△ABC中,AC=BC=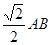 ,四边形ABED是正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点。
,四边形ABED是正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点。