题目内容
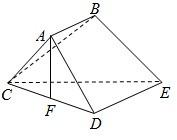 如图,多面体ABCDE中,四边形ABED是直角梯形,∠BAD=90°,DE∥AB,平面BAED^平面ACD,△ACD是边长为2a的正三角形,DE=2AB=2a,F是CD的中点
如图,多面体ABCDE中,四边形ABED是直角梯形,∠BAD=90°,DE∥AB,平面BAED^平面ACD,△ACD是边长为2a的正三角形,DE=2AB=2a,F是CD的中点(Ⅰ)求证:AF⊥平面CDE;
(Ⅱ)求面ACD与面BCE所成二面角的大小.
分析:(I)由已知中,∠BAD=90°,DE∥AB,结合平面BAED⊥平面ACD,易得到DE⊥面ACD,DE⊥AF,又由F是CD的中点,根据等腰三角形三线合一得AF⊥CD,结合线面垂直的判定定理即可得到答案.
(II)延长DA,EB相交于点G,连接CG,根据平行线分线段成比例定理,我们及判断出AF∥CG,结合(1)的结论,我们易得∠DCE为面ACD与面BCE所成二面角的平面角,解三角形ACD,即可得到答案.
(II)延长DA,EB相交于点G,连接CG,根据平行线分线段成比例定理,我们及判断出AF∥CG,结合(1)的结论,我们易得∠DCE为面ACD与面BCE所成二面角的平面角,解三角形ACD,即可得到答案.
解答: (Ⅰ)证明:∵∠BAD=90°,DE∥AB,∴DE⊥AD
(Ⅰ)证明:∵∠BAD=90°,DE∥AB,∴DE⊥AD
又平面BAED⊥平面ACD,平面BAED∩平面ACD=AD,∴DE⊥面ACD,∴DE⊥AF(3分)
∵DACD是正三角形,F是CD的中点,
∴AF⊥CD,
∴AF⊥平面CDE.(6分)
(Ⅱ)解:延长DA,EB相交于点G,连接CG,
易知平面ACD∩平面BCE=GC
由DE∥ABB,DE=2AB=2a知
=
=
∴
=
∵F是CD的中点,∴
=
,
∴
=
?AF∥CG
由(Ⅰ)AF⊥平面CDE,∴GC⊥平面CDE
∴GC⊥CD,GC⊥CE
∴∠DCE为面ACD与面BCE所成二面角的平面角 (9分)
在DCDE中,∠CDE=90°,DE=CD=2a,∴∠DCE=45°
即面ACD与面BCE所成二面角为45° (12分)
 (Ⅰ)证明:∵∠BAD=90°,DE∥AB,∴DE⊥AD
(Ⅰ)证明:∵∠BAD=90°,DE∥AB,∴DE⊥AD又平面BAED⊥平面ACD,平面BAED∩平面ACD=AD,∴DE⊥面ACD,∴DE⊥AF(3分)
∵DACD是正三角形,F是CD的中点,
∴AF⊥CD,
∴AF⊥平面CDE.(6分)
(Ⅱ)解:延长DA,EB相交于点G,连接CG,
易知平面ACD∩平面BCE=GC
由DE∥ABB,DE=2AB=2a知
| GA |
| GD |
| AB |
| DE |
| 1 |
| 2 |
∴
| DA |
| DG |
| 1 |
| 2 |
∵F是CD的中点,∴
| DF |
| DC |
| 1 |
| 2 |
∴
| DA |
| DG |
| DF |
| DC |
由(Ⅰ)AF⊥平面CDE,∴GC⊥平面CDE
∴GC⊥CD,GC⊥CE
∴∠DCE为面ACD与面BCE所成二面角的平面角 (9分)
在DCDE中,∠CDE=90°,DE=CD=2a,∴∠DCE=45°
即面ACD与面BCE所成二面角为45° (12分)
点评:本题考查的知识点是直线与平面垂直的判定,二面角的平面角的求法,熟练掌握空间直线与平面位置关系的判定、性质、定义及几何特征是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


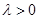 使得
使得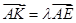 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为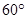 ,求
,求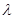 的值。
的值。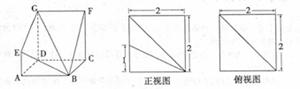
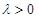 使得
使得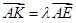 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为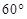 ,求
,求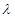 的值。
的值。
 使得
使得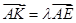 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为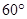 ,求
,求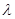 的值。
的值。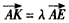 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。