题目内容
已知实数x,y同时满足4-x+27-y=
,log27y-log4x≥
,27y-4x≤1,则x+y的取值范围是
| 5 |
| 6 |
| 1 |
| 6 |
{
}
| 5 |
| 6 |
{
}
.| 5 |
| 6 |
分析:题目给出了一个等式和两个不等式,分析给出的等式的特点,得到当x=
,y=
时该等式成立,同时把相应的x和y的值代入后面的两个不等式等号也成立,把给出的等式的左边变负指数幂为正指数幂,分析x和y的变化规律,知道y随x的增大而减小,而当x增大y减小时,两不等式不成立,因此断定,同时满足等式和不等式的x,y取值唯一,从而可得x+y的取值范围.
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:当x=
,y=
时,
4-x+27-y=4-
+27-
=
+
=
,
log27y-log4x=log27
-log4
=-
+
=
,
27y-4x=27
-4
=3-2=1.
由4-x+27-y=
+
=
知,等式右边一定,左边y随x的增大而减小,
而当y减小x增大时,log27y-log4x<
,
当x减小y增大时,27y-4x>1.
均与题中所给条件不等式矛盾.
综上,只有x=
,y=
时,条件成立,
所以x+y的取值范围为{
}.
故答案为{
}.
| 1 |
| 2 |
| 1 |
| 3 |
4-x+27-y=4-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
log27y-log4x=log27
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
27y-4x=27
| 1 |
| 3 |
| 1 |
| 2 |
由4-x+27-y=
| 1 |
| 4x |
| 1 |
| 27y |
| 5 |
| 6 |
而当y减小x增大时,log27y-log4x<
| 1 |
| 6 |
当x减小y增大时,27y-4x>1.
均与题中所给条件不等式矛盾.
综上,只有x=
| 1 |
| 2 |
| 1 |
| 3 |
所以x+y的取值范围为{
| 5 |
| 6 |
故答案为{
| 5 |
| 6 |
点评:本题考查了有理指数幂的化简与求值,考查了对数式的运算性质,考查了特值验证法,培养了学生的探究能力,此题是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
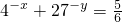 ,
,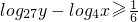 ,27y-4x≤1,则x+y的取值范围是________.
,27y-4x≤1,则x+y的取值范围是________. ,
, ,27y-4x≤1,则x+y的取值范围是 .
,27y-4x≤1,则x+y的取值范围是 . ,
, ,27y-4x≤1,则x+y的取值范围是 .
,27y-4x≤1,则x+y的取值范围是 .