题目内容
(本小题满分14分)
已知函数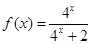 .
.
(Ⅰ)求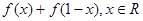 的值;
的值;
(Ⅱ)若数列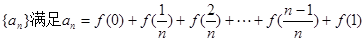
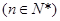 ,
,
求数列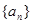 的通项公式;
的通项公式;
(Ⅲ)若数列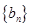 满足
满足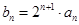 ,
,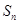 是数列
是数列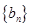 的前
的前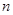 项和,是否存在正实数
项和,是否存在正实数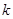 ,使不等式
,使不等式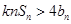 对于一切的
对于一切的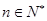 恒成立?若存在,请求出
恒成立?若存在,请求出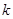 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知函数
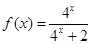 .
.(Ⅰ)求
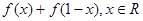 的值;
的值;(Ⅱ)若数列
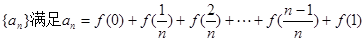
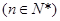 ,
,求数列
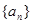 的通项公式;
的通项公式;(Ⅲ)若数列
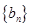 满足
满足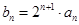 ,
,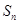 是数列
是数列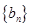 的前
的前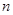 项和,是否存在正实数
项和,是否存在正实数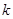 ,使不等式
,使不等式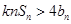 对于一切的
对于一切的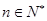 恒成立?若存在,请求出
恒成立?若存在,请求出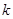 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.解:(1)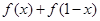 =1;(2)
=1;(2)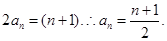 (3)
(3)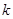
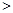
 .
.
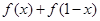 =1;(2)
=1;(2)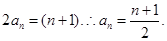 (3)
(3)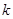
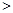
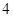 .
.试题分析:(1)由f(x)+f(1-x)= =1,能得到f(
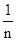 )+f(
)+f( 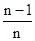 )=1.由此规律求值即可
)=1.由此规律求值即可(2)由an=f(0)+f(
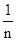 )+f(
)+f(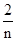 )+…+f(
)+…+f(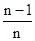 )+f(1)(n∈N*),知an=f(1)+f(
)+f(1)(n∈N*),知an=f(1)+f(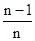 )+f(
)+f( )+…+f(
)+…+f(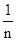 )+f(0)(n∈N*),由倒序相加法能得到an
)+f(0)(n∈N*),由倒序相加法能得到an(3)由bn=2n+1•an,知bn=(n+1)•2n,由Sn=2•21+3•22+4•23+…+(n+1)•2n,利用错位相减法能求出Sn=n•2n+1,要使得不等式knSn>4bn恒成立,即kn2-2n-2>0对于一切的n∈N*恒成立,由此能够证明当k>4时,不等式knSn>bn对于一切的n∈N*恒成立.
解:(1)
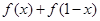 =
=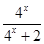 +
+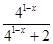 =
=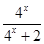 +
+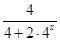 =1
=1(2)∵
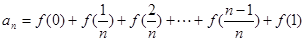 ①
①∴
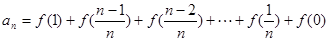 ②
②由(Ⅰ),知
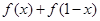 =1
=1∴①+②,得
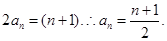
(3)∵
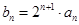 ,∴
,∴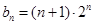
∴
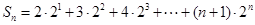 , ①
, ① , ②
, ②①-②得
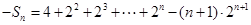
即
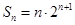 要使得不等式
要使得不等式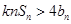 恒成立,即
恒成立,即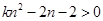 对于一切的
对于一切的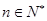 恒成立,
恒成立,法一:
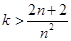 对一切的
对一切的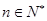 恒成立,
恒成立,令
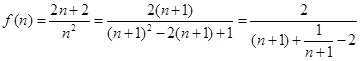 ,
,∵
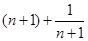 在
在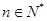 是单调递增的, ∴
是单调递增的, ∴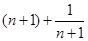 的最小值为
的最小值为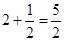
∴
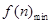 =
= , ∴
, ∴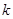
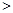
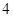 .
.法二:
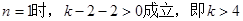 . 设
. 设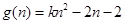
当
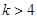 时,由于对称轴直线
时,由于对称轴直线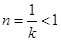 ,且
,且 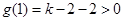 ,而函数
,而函数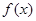 在
在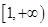 是增函数, ∴不等式
是增函数, ∴不等式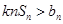 恒成立
恒成立 即当
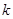
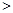
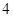 时,不等式
时,不等式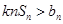 对于一切的
对于一切的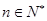 恒成立
恒成立点评:解题时要注意倒序相加法、错位相减法的灵活运用.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
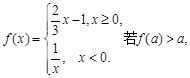 则实数
则实数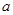 的取值范围是( )
的取值范围是( )


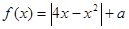 有4个零点,则实数
有4个零点,则实数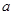 的取值范围是______.
的取值范围是______.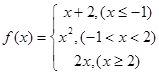 ,则
,则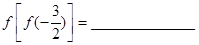
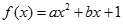 (
(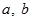 为实数,
为实数,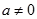 ,
,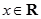 ),若
),若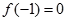 ,且函数
,且函数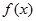 的值域为
的值域为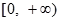 .
. 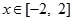 时,
时,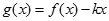 是单调函数,求实数
是单调函数,求实数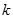 的取值范围.
的取值范围. 满足:x≥4,
满足:x≥4, ;当x<4时
;当x<4时 ,则
,则 =
=



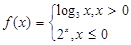 ,则
,则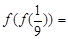 ;
; 且任意的
且任意的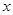 、
、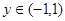 都有
都有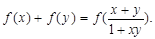
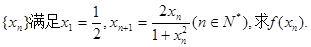
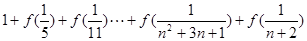 的值.
的值. 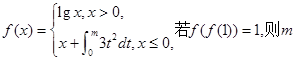 = ;
= ;