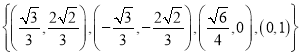题目内容
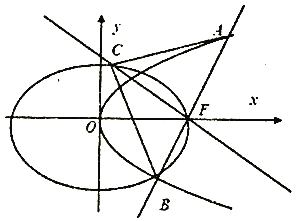
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() ,
,![]() ,
,![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)若![]() .①当
.①当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
②证明![]() 是定值,并求出此定值.
是定值,并求出此定值.
【答案】(1)![]() ;(2)①
;(2)①![]() 或
或![]() ;②证明见解析,
;②证明见解析,![]() .
.
【解析】
(1)根据![]() 周长和焦点坐标可得到关于
周长和焦点坐标可得到关于![]() 的方程组,解方程组求得
的方程组,解方程组求得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)设直线![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() 与
与![]() ;
;
①由![]() 可得
可得![]() ,代入
,代入![]() 与
与![]() 中,消去
中,消去![]() 即可得到关于
即可得到关于![]() 的方程,解方程求得
的方程,解方程求得![]() ,即可得到所求直线方程;
,即可得到所求直线方程;
②利用焦半径公式可表示出![]() 和
和![]() ,从而将所证明式子表示为
,从而将所证明式子表示为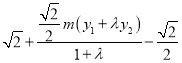 ,代入
,代入![]() 可化简得到定值为
可化简得到定值为![]() .
.
(1)![]() 的周长为
的周长为![]()
![]() ,又
,又![]()
解得:![]() ,
,![]()
![]() 椭圆的标准方程为
椭圆的标准方程为![]()
(2)设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
,![]()
把![]() 代入
代入![]() 并化简得:
并化简得:![]()
则有![]() ,
,![]()
①当![]() 时,由
时,由![]() 可得:
可得:![]() ,则
,则![]() ,
,![]()
消去![]() 得:
得: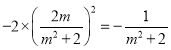 ,解得:
,解得:![]()
![]() 直线
直线![]() 的方程为
的方程为![]() 或
或![]() ;
;
②由题意得:![]()
![]()
![]() ,
,![]()
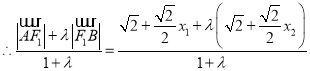
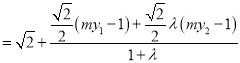
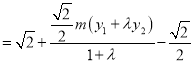
由![]() 可得
可得![]() ,代入上式得:
,代入上式得: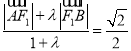
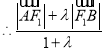 是定值,定值为
是定值,定值为![]()

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目