题目内容
13.已知函数f(x)=$\frac{p{x}^{2}+2}{q{x}^{2}-2x}$是奇函数,且f(1)=-2.(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,1)上的单调性,并加以证明.
分析 (1)根据函数f(x)=$\frac{p{x}^{2}+2}{q{x}^{2}-2x}$是奇函数,可得f(-x)=-f(x)恒成立,结合f(1)=-2,求出p,q,可得函数f(x)的解析式;
(2)函数f(x)在(0,1)上是单调递增的,利用导数法,易证得结论.
解答 解:(1)∵函数f(x)=$\frac{p{x}^{2}+2}{q{x}^{2}-2x}$是奇函数,
∴f(-x)=-f(x),
即$\frac{p{x}^{2}+2}{q{x}^{2}+2x}$=-$\frac{p{x}^{2}+2}{q{x}^{2}-2x}$,
解得:q=0,
又∵f(1)=-2.
∴$\frac{p+2}{-2}$=-2,
∴p=2,
∴f(x)=$\frac{2{x}^{2}+2}{-2x}$=$-\frac{{x}^{2}+1}{x}$;
(2)函数f(x)在(0,1)上是单调递增的,理由如下:
∵f(x)=$-\frac{{x}^{2}+1}{x}$;
∴f′(x)=$\frac{1-{x}^{2}}{{x}^{2}}$,
当x∈(0,1)时,f′(x)>0恒成立,
故函数f(x)在(0,1)上是单调递增的.
点评 本题考查的知识点是函数单调性及奇偶性,函数解析式的求法,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知全集U={x∈Z|x2-3x-10<0},集合P={0,3},Q=|2,0,1},则∁U(P∪Q)=( )
| A. | {-1,4,5} | B. | {-1,4} | C. | {-1,1,2,3,4} | D. | {1,2,3} |
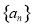 中,
中,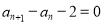 ,且
,且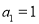 ,则
,则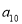 等于( )
等于( )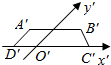 (1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.
(1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.