题目内容
19.若直线y=k(x+1)上存在点(x,y)满足约束条件$\left\{\begin{array}{l}{x-y+\sqrt{3}≥0}\\{\sqrt{3}x-y-\sqrt{3}≤0}\\{y≥\sqrt{3}}\\{\;}\end{array}\right.$,则直线y=k(x+1)的倾斜角的取值范围为$[{\frac{π}{6},\frac{π}{3}}]$.分析 由约束条件作出可行域,求出直线所过定点,求出直线与可行域中点连线斜率的最小值和最大值,再由斜率等于直线倾斜角的正切值得答案.
解答 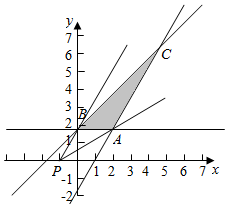 解:由约束条件$\left\{\begin{array}{l}{x-y+\sqrt{3}≥0}\\{\sqrt{3}x-y-\sqrt{3}≤0}\\{y≥\sqrt{3}}\end{array}\right.$作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}{x-y+\sqrt{3}≥0}\\{\sqrt{3}x-y-\sqrt{3}≤0}\\{y≥\sqrt{3}}\end{array}\right.$作出可行域如图,
直线y=k(x+1)过定点P(-1,0),
由图可知A($2,\sqrt{3}$),B(0,$\sqrt{3}$),
则${k}_{PA}=\frac{\sqrt{3}}{3},{k}_{PB}=\sqrt{3}$,
∴直线PA的倾斜角为$\frac{π}{6}$,直线PB的倾斜角为$\frac{π}{3}$.
则函数y=k(x+1)表示的直线的倾斜角的取值范围为$[\frac{π}{6},\frac{π}{3}]$.
故答案为:$[{\frac{π}{6},\frac{π}{3}}]$.
点评 本题主要考查线性规划的应用以及直线斜率的求解,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
4.已知函数f(x)=sin(2x+φ)在x=$\frac{π}{6}$处取得极大值,则函数y=f($\frac{π}{4}$+x)的图象( )
| A. | 关于点($\frac{π}{6}$,0)对称 | B. | 关于点($\frac{π}{3}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{3}$对称 |
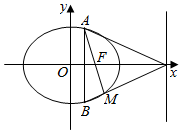 如图,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,F为该椭圆的右焦点,若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M(x0,y0).
如图,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,F为该椭圆的右焦点,若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M(x0,y0).