题目内容
(本小题满分12分)
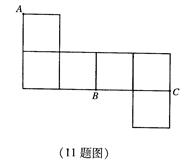
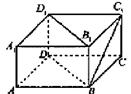
如图,在直三棱柱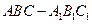 中,平面
中,平面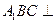 侧面。
侧面。
(Ⅰ)求证: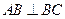 ;
;
(Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ,试判断θ与φ的大小关系,并予以证明。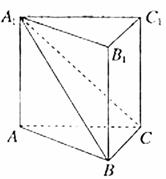
如图,在直三棱柱
 中,平面
中,平面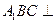 侧面。
侧面。(Ⅰ)求证:
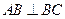 ;
;(Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ,试判断θ与φ的大小关系,并予以证明。

(Ⅰ)证明见解析。
(Ⅱ)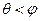 ,证明见解析。
,证明见解析。
(Ⅱ)
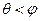 ,证明见解析。
,证明见解析。(Ⅰ)证明:如右图,过点A在平面A1ABB1内作AD⊥A1B于D,则
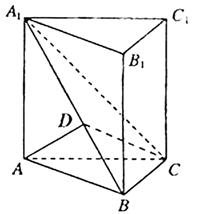
由平面A1BC⊥侧面A1ABB1,且平面A1BC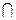 侧面A1ABB1=A1B,得
侧面A1ABB1=A1B,得
AD⊥平面A1BC,又BC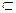 平面A1BC,所以AD⊥BC。
平面A1BC,所以AD⊥BC。
因为三棱柱ABC—A1B1C1是直三棱柱,则AA1⊥底面ABC,所以AA1⊥BC。
又AA1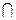 AD=A,从而BC⊥侧面A1ABB1,
AD=A,从而BC⊥侧面A1ABB1,
又AB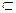 侧面A1ABB1,故AB⊥BC。
侧面A1ABB1,故AB⊥BC。
(Ⅱ)解法1:连接CD,则由(Ⅰ)知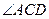 是直线AC与平面A1BC所成的角,
是直线AC与平面A1BC所成的角,
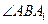 是二面角A1—BC—A的平面角,即
是二面角A1—BC—A的平面角,即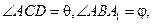
于是在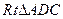 中,
中,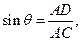 在
在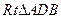 中,
中,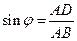 ,
,
由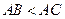 ,得
,得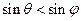 ,又
,又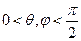 ,所以
,所以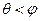 。
。
解法2:由(1)知,以点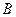 为坐标原点,以
为坐标原点,以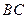 、
、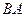 、
、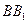 所在的直线分
所在的直线分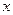 轴、
轴、 轴、
轴、 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
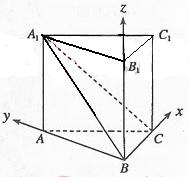
设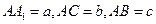 ,
,
则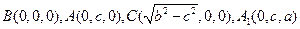 ,
,
于是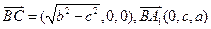 ,
,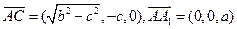 。
。
设平面的一个法向量为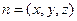 ,则
,则
由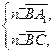 得
得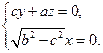
可取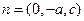 ,于是
,于是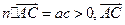 与
与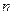 的夹角
的夹角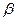 为锐角,则
为锐角,则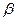 与
与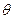 互为余角。
互为余角。
所以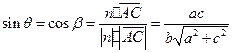 ,
,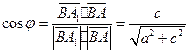 ,
,
所以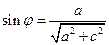 。
。
于是由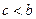 ,得
,得 ,
,
即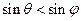 ,又
,又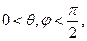 所以
所以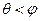 。
。
第(1)问证明线线垂直,一般先证线面垂直,再由线面垂直得线线垂直;第(2)问若用传统方法一般来说要先作垂直,进而得直角三角形。若用向量方法,关键在求法向量。

由平面A1BC⊥侧面A1ABB1,且平面A1BC
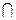 侧面A1ABB1=A1B,得
侧面A1ABB1=A1B,得AD⊥平面A1BC,又BC
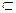 平面A1BC,所以AD⊥BC。
平面A1BC,所以AD⊥BC。因为三棱柱ABC—A1B1C1是直三棱柱,则AA1⊥底面ABC,所以AA1⊥BC。
又AA1
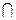 AD=A,从而BC⊥侧面A1ABB1,
AD=A,从而BC⊥侧面A1ABB1,又AB
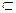 侧面A1ABB1,故AB⊥BC。
侧面A1ABB1,故AB⊥BC。(Ⅱ)解法1:连接CD,则由(Ⅰ)知
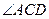 是直线AC与平面A1BC所成的角,
是直线AC与平面A1BC所成的角,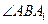 是二面角A1—BC—A的平面角,即
是二面角A1—BC—A的平面角,即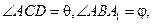
于是在
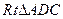 中,
中,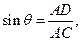 在
在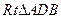 中,
中,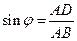 ,
,由
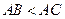 ,得
,得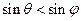 ,又
,又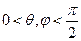 ,所以
,所以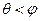 。
。解法2:由(1)知,以点
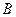 为坐标原点,以
为坐标原点,以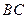 、
、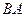 、
、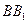 所在的直线分
所在的直线分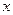 轴、
轴、 轴、
轴、 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
设
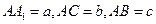 ,
,则
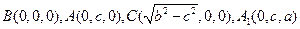 ,
,于是
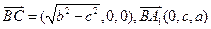 ,
,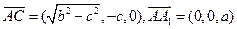 。
。设平面的一个法向量为
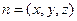 ,则
,则由
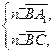 得
得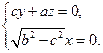
可取
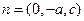 ,于是
,于是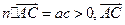 与
与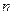 的夹角
的夹角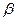 为锐角,则
为锐角,则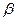 与
与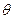 互为余角。
互为余角。所以
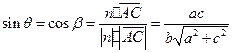 ,
,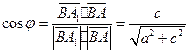 ,
,所以
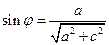 。
。于是由
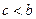 ,得
,得 ,
,即
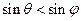 ,又
,又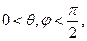 所以
所以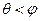 。
。第(1)问证明线线垂直,一般先证线面垂直,再由线面垂直得线线垂直;第(2)问若用传统方法一般来说要先作垂直,进而得直角三角形。若用向量方法,关键在求法向量。

练习册系列答案
相关题目

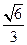
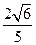
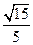
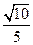
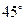 纬线上有A,B两点,设该纬线圈上A,B两点的劣弧长为
纬线上有A,B两点,设该纬线圈上A,B两点的劣弧长为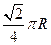 ,(R为地球半径),则A,B两点间的球面距离为__________________.
,(R为地球半径),则A,B两点间的球面距离为__________________.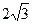 ,侧棱与底面所成的角为
,侧棱与底面所成的角为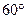 ,则该棱锥的体积为( )
,则该棱锥的体积为( )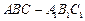 中,
中,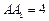 ,
,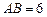 ,点
,点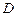 、
、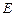 、
、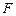 分别在棱
分别在棱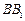 、
、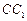 、
、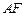 上,且
上,且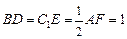 .
.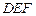 与平面
与平面 所成锐二面角的大小;
所成锐二面角的大小; 到平面
到平面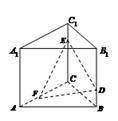
 ,直线
,直线 ,给出下列命题
,给出下列命题 ∥
∥ ;②
;② ∥m;③
∥m;③ ∥
∥ ;④
;④ ∥
∥ .
.
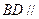 平面
平面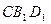
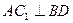
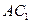 与
与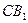 角为60°
角为60°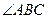 的度数为 .
的度数为 .