题目内容
【题目】设函数![]() 的定义域为
的定义域为![]() ,其中
,其中![]() ,
,![]() .
.
(1)若![]() ,判断
,判断![]() 的单调性;
的单调性;
(2)当![]() ,设函数
,设函数![]() 在区间
在区间![]() 上恰有一个零点,求正数a的取值范围;
上恰有一个零点,求正数a的取值范围;
(3)当![]() ,
,![]() 时,证明:对于
时,证明:对于![]() ,有
,有 .
.
【答案】(1)见解析;(2)![]() (3)见解析
(3)见解析
【解析】
(1)由题意求导后,按照![]() 、
、![]() 分类,解出
分类,解出![]() 、
、![]() 的解集即可得解;
的解集即可得解;
(2)对![]() 求导,令
求导,令![]() ,求导后可得
,求导后可得![]() 在
在![]() 上单调递减,按照
上单调递减,按照![]() 、
、![]() ,结合函数单调性、零点存在性定理即可得解;
,结合函数单调性、零点存在性定理即可得解;
(3)令![]() ,求导后可得对
,求导后可得对![]() ,恒有
,恒有![]() ,依次取
,依次取![]() ,求和即可得证.
,求和即可得证.
(1)![]() 时,
时,![]() ,
,![]() ,
,
则![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,令
时,令![]() ,
,![]() ,
,![]() (舍),
(舍),
令![]() ,
, ,
,![]() ,
,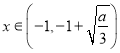
∴函数![]() 的单调增区间为
的单调增区间为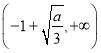 ,单调减区间为
,单调减区间为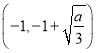 ;
;
综上,当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为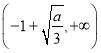 ,单调减区间为
,单调减区间为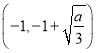 ;
;
(2)由题意![]() ,则
,则![]() ,
,
令![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,
,
①若![]() ,则
,则![]() 即
即![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,∴
,∴![]() ,不合题意;
,不合题意;
②若![]() ,则
,则![]() ,
,![]() ,
,
∴根椐零点存在性定理![]() ,使得
,使得![]() ,
,
即![]() ,使得
,使得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
∴![]() ,函数
,函数![]() 无零点;
无零点;
当![]() 时,
时, ![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
其中![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,∴
上单调递减,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
根据零点存在性定理可得![]() 时有且仅有一个零点,符合题意;
时有且仅有一个零点,符合题意;
综上:![]() ;
;
(3)当![]() 时,令
时,令![]() ,则
,则![]()
当![]() 时,恒有
时,恒有![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 对
对![]() 恒成立.
恒成立.
又![]() ,
,![]() ,故
,故![]() ,
,
即对![]() ,恒有
,恒有![]() ,
,
在此不等式中依次取![]() ,得:
,得:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
将以上不等式相加得: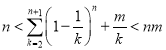 ,即
,即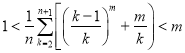 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.

(1)求出易倒伏玉米茎高的中位数![]() ;
;
(2)根据茎叶图的数据,完成下面的列联表:
抗倒伏 | 易倒伏 | |
矮茎 | ||
高茎 |
(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
附: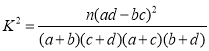 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某校在高一年级一班至六班进行了“社团活动”满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 4 | 5 | 11 | 8 | 10 | 12 |
满意人数 | 3 | 2 | 8 | 5 | 6 | 6 |
现从一班和二班调查对象中随机选取4人进行追踪调查,则选中的4人中恰有2人不满意的概率为___________;若将以上统计数据中学生持满意态度的频率视为概率,在高一年级全体学生中随机抽取3名学生,记其中满意的人数为X,则随机变量X的数学期望是___________