题目内容
如图所示，ABCD是一个矩形花坛，其中AB=4米，AD=3米．现将矩形花坛ABCD扩建成一个更大的矩形花园AMPN，要求：B在AM上，D在AN上，对角线MN过C点，且矩形AMPN的面积小于64平方米．（1）设AN长为x米，矩形AMPN的面积为S平方米，试用解析式将S表示成x的函数，并写出该函数的定义域；
（2）当AN的长度是多少时，矩形AMPN的面积最小？并求最小面积．
分析：（1）由△NDC∽△NAM，可得
=
，可得AM=
，得到S=AN•AM=
，令S＜64即可得到定义域；
（2）由（1），通过换元，利用基本不等式即可得出．
| DN |
| NA |
| DC |
| AM |
| 4x |
| x-3 |
| 4x2 |
| x-3 |
（2）由（1），通过换元，利用基本不等式即可得出．
解答：
解：（1）由△NDC∽△NAM，可得
=
，
∴
=
，即AM=
，
故S=AN•AM=
，
由S=
＜64且x＞3，解得4＜x＜12，
故所求函数的解析式为S=
，定义域为（4，12）．
（2）令x-3=t，则由x∈（4，12），可得t∈（1，9），
故S=
=
=4(t+
+6)≥4(2
+6)=48，
当且仅当t=
，即t=3时，即当x=6时，S取最小值48．
故当AN的长为6时，矩形AMPN的面积最小，最小面积为48平方米．
解：（1）由△NDC∽△NAM，可得| DN |
| NA |
| DC |
| AM |
∴
| x-3 |
| x |
| 4 |
| AM |
| 4x |
| x-3 |
故S=AN•AM=
| 4x2 |
| x-3 |
由S=
| 4x2 |
| x-3 |
故所求函数的解析式为S=
| 4x2 |
| x-3 |
（2）令x-3=t，则由x∈（4，12），可得t∈（1，9），
故S=
| 4x2 |
| x-3 |
| 4(t+3)2 |
| t |
| 9 |
| t |
t•
|
当且仅当t=
| 9 |
| t |
故当AN的长为6时，矩形AMPN的面积最小，最小面积为48平方米．
点评：本题考查了相似三角形的性质、矩形的面积、基本不等式的性质，属于中档题．
练习册系列答案
相关题目
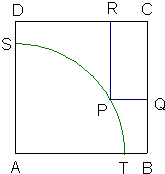如图所示，ABCD是一块边长为100米的正方形地皮，其中ATPS是一个半径为90米的扇形小山，P是弧TS上一点，其余都是平地．现要在平地上建造矩形停车场PQCR，求停车场PQCR的最大面积．
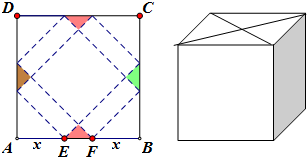请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上，是被切去的等腰直角三角形斜边的两个端点，设AE=FB=x（cm）．
11、如图所示，ABCD是一个平面图形的斜二侧直观图，则该图形是（ ）
如图所示，ABCD是一平面图形的水平放置的斜二侧直观图．在斜二侧直观图中，ABCD是一直角梯形，AB∥CD，AD⊥CD，且BC与y轴平行．若AB=6，AD=2，则这个平面图形的实际面积为（ ）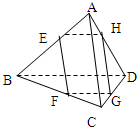
如图所示，ABCD是空间四边形，E、F、G、H分别是四边上的中点，并且AC⊥BD，AC=m，BD=n，则四 边形EFGH的面积为