Question

已知a＞1,b＞1,c＞1,且ab=10,求证:log_ac+log_bc≥4lgc.

Answer 1

分析：这是一个条件不等式,证明时要充分考虑条件的使用,另外若遇到和式或积式可考虑运用均值定理去放缩.

证明：∵a＞1,b＞1,c＞1,

故lga＞0,lgb＞0,lgc＞0.

∴log_ac+log_bc=+≥2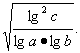

∵ab=10,故lg(ab)=1,即lga+lgb=1.

∴lga·lgb≤=,

故log_ac+log_bc≥2=4lgc,

即log_ac+log_bc≥4lgc.