已知正项等差数列{an}满足a1+a2017=2.则$\frac{1}{a 2}+\frac{1}{{{a {2016}}}}$的最小值为( )A．1B．2C．2016D．2018 题目和参考答案——青夏教育精英家教网——

题目内容

7．已知正项等差数列{a_n}满足a₁+a₂₀₁₇=2，则$\frac{1}{a_2}+\frac{1}{{{a_{2016}}}}$的最小值为（　　）

A．

1

B．

2

C．

2016

D．

2018

分析正项等差数列{a_n}满足a₁+a₂₀₁₇=2，可得a₂+a₂₀₁₆=a₁+a₂₀₁₇=2，化简利用基本不等式的性质即可得出．

解答解：∵正项等差数列{a_n}满足a₁+a₂₀₁₇=2，
∴a₂+a₂₀₁₆=a₁+a₂₀₁₇=2，
则$\frac{1}{a_2}+\frac{1}{{{a_{2016}}}}$=$\frac{{a}_{2}+{a}_{2016}}{{a}_{2}{a}_{2016}}$=$\frac{2}{{a}_{2}{a}_{2016}}$≥$\frac{2}{（\frac{{a}_{1}+{a}_{2017}}{2}）^{2}}$=2，当且仅当a₁=a₂₀₁₇时取等号．
故选：B．

点评本题考查了等差数列的通项公式性质、基本不等式的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案

经纶学典提高班系列答案

普通高中新课程问题导学案系列答案

开心蛙状元测试卷系列答案

名牌牛皮卷提优名卷系列答案

海淀黄冈全程大考卷系列答案

金榜1卷通系列答案

启东黄冈小状元系列答案

江苏正卷系列答案

悦然好学生周周测系列答案

单元加期末复习与测试系列答案

相关题目

已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的右焦点到直线x-y+3$\sqrt{2}$=0的距离为5，且椭圆的一个长轴端点与一个短轴端点间的距离为$\sqrt{10}$．
（1）求椭圆C的方程；
（2）如图，连接椭圆短轴端点A与椭圆上不同于A的两点M，N，与以椭圆短轴为直径的圆分别交于P，Q两点，且PQ恰好经过圆心O，求△AMN面积的最大值．

18．向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$在单位正方形网格中的位置如图所示，则$\overrightarrow{a}$•（$\overrightarrow{b}$+$\overrightarrow{c}$）=3．

15．下面几个数中：①3^0.4；②$\frac{1+tan15°}{1-tan15°}$；③log₂3•log₉8；④5^0.2；⑤3${\;}^{\frac{1}{3}}$，最大的是②，最小的是④（请填写对应数的序号）

2．某次知识竞赛中，四个参赛小队的初始积分都是100分，在答题过程中，各小组每答对1题都可以使自己小队的积分增加5分，若答题过程中四个小队答对的题数分别是4道，7道，7道，2道，则四个小组积分的方差为（　　）

12．已知函数f（x）=x²-2，对?x₁∈[1，2]，?x₂∈[3，4]，若f（x₂）+a≥|f（x₁）|恒成立，则实数a的取值范围是[-12，+∞）．

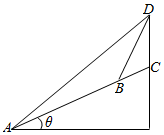如图所示，在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD，为了测量该山坡相对于水平地面的坡角θ，在山坡的A处测得∠DAC=15°，沿山坡前进50m到达B处，又测得∠DBC=45°，根据以上数据可得cosθ=$\sqrt{3}$-1．

16．若a，b都是不等于1的正数，则“log_a2＞log_b2”是“2^a＞2^b”的（　　）

	A．	充分非必要条件		B．	必要非充分条件
	C．	充要条件		D．	非充分非必要条件

如图所示，在四边形ABCD中，cosB=$\frac{\sqrt{3}}{3}$，∠D=2∠B，AD=1，且△ACD的面积为$\sqrt{2}$
（1）求CD的长度；
（2）若BC=2$\sqrt{3}$，求AB的长．