题目内容
(本小题满分12分)
已知抛物线y2=mx的焦点到准线距离为1,且抛物线开口向右.
(Ⅰ)求m的值;
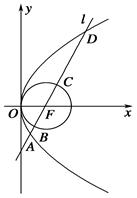
(Ⅱ)P是抛物线y2=mx上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于
△PBC,求△PBC面积的最小值.
已知抛物线y2=mx的焦点到准线距离为1,且抛物线开口向右.
(Ⅰ)求m的值;
(Ⅱ)P是抛物线y2=mx上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于
△PBC,求△PBC面积的最小值.
(1)
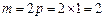
(2)
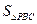 的最小值为8.
的最小值为8.解:(Ⅰ)由题意知,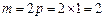 .……………………4分
.……………………4分
(Ⅱ)设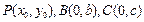 ,不妨设
,不妨设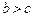 .直线
.直线 的方程:
的方程: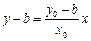 ,
,
化简得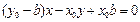 .
.
又圆心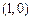 到
到 的距离为1,
的距离为1,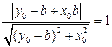 ,
,
故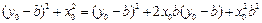 ,…………………6分
,…………………6分
易知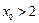 ,上式化简得
,上式化简得 ,
,
同理有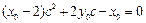 .
.
所以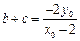 ,
,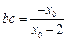 ,则
,则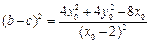 .……………8分
.……………8分
因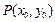 是抛物线上的点,有
是抛物线上的点,有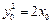 ,则
,则 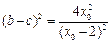 ,
,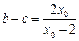 .
.
所以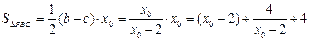
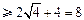 .……10分
.……10分
当 时,上式取等号.
时,上式取等号.
此时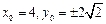 .∴
.∴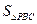 的最小值为8.………………………… 12分
的最小值为8.………………………… 12分
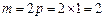 .……………………4分
.……………………4分(Ⅱ)设
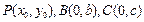 ,不妨设
,不妨设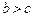 .直线
.直线 的方程:
的方程: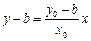 ,
,化简得
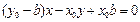 .
.又圆心
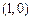 到
到 的距离为1,
的距离为1,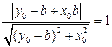 ,
, 故
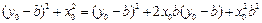 ,…………………6分
,…………………6分易知
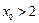 ,上式化简得
,上式化简得 ,
, 同理有
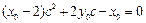 .
. 所以
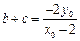 ,
,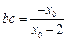 ,则
,则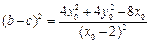 .……………8分
.……………8分因
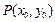 是抛物线上的点,有
是抛物线上的点,有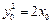 ,则
,则 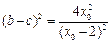 ,
,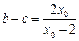 .
. 所以
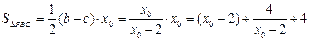
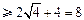 .……10分
.……10分当
 时,上式取等号.
时,上式取等号.此时
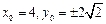 .∴
.∴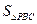 的最小值为8.………………………… 12分
的最小值为8.………………………… 12分 
练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
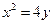 的对称轴上任一点
的对称轴上任一点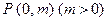 作直线与抛物线交于
作直线与抛物线交于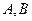 两点,点
两点,点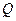 是点
是点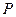 关于原点的对称点.
关于原点的对称点.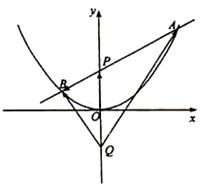
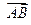 所成的比为
所成的比为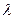 ,证明:
,证明:
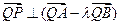 ;
;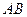 的方程是
的方程是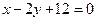 ,过
,过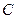 与抛物线在点
与抛物线在点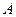 处有共同的切线,求圆
处有共同的切线,求圆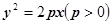 上一点P到准线和抛物线的对称轴的距离分别为10和6,则此点P的横坐标为 ( )
上一点P到准线和抛物线的对称轴的距离分别为10和6,则此点P的横坐标为 ( )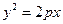 x上横坐标为4的点到该抛物线的焦点的距离为5。
x上横坐标为4的点到该抛物线的焦点的距离为5。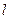 交抛物线C于A、B两点,求证:
交抛物线C于A、B两点,求证: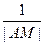 +
+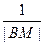 恒为定值。
恒为定值。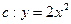 的焦点为F,准线
的焦点为F,准线 为
为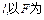
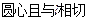 的圆与该抛物线相交于
的圆与该抛物线相交于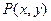 在由直线y=2,y
在由直线y=2,y =4和抛物线
=4和抛物线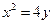 所围成的平面区域内(含边界)则
所围成的平面区域内(含边界)则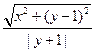 的取值范围为
的取值范围为  分别为过抛物线
分别为过抛物线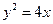 的焦点
的焦点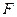 的直线与该抛物线和圆
的直线与该抛物线和圆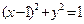 的交点,则
的交点,则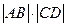 等于 ( )
等于 ( )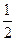

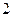
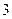
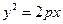 上,横坐标为4的点到焦点的距离为5,则
上,横坐标为4的点到焦点的距离为5,则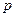 的值为___________
的值为___________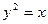 的焦点F,与抛物线相交于A、B两点,且|AB|=3,则线段AB的中点到y轴的距离为( )
的焦点F,与抛物线相交于A、B两点,且|AB|=3,则线段AB的中点到y轴的距离为( )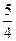 C.
C.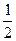 D.2
D.2