题目内容
建造一个容积为6400立方米,深为4米的长方体无盖蓄水池,池壁的造价为每平方米200元,池底的造价为每平方米100元.
(1)把总造价y元表示为池底的一边长x米的函数;
(2)蓄水池的底边长为多少时总造价最低?总造价最低是多少?
(1)把总造价y元表示为池底的一边长x米的函数;
(2)蓄水池的底边长为多少时总造价最低?总造价最低是多少?
分析:(1)水池总造价函数为y=池底造价+池壁造价,代入整理即可;
(2)由(1)得出总造价函数y=1600(x+
)+160000,应用函数单调性的定义研究其单调性,从而得出这个函数在(0,40]上是减函数,在[40,+∞)增函数,可求得函数的最小值以及对应的x的值.
(2)由(1)得出总造价函数y=1600(x+
| 1600 |
| x |
解答:解:(1)由已知池底的面积为1600平方米,底面的另一边长为
米,--------(1分)
则池壁的面积为8(x+
)平方米.------------------------------------(3分)
所以总造价:y=1600(x+
)+160000(元),x∈(0,+∞).-------------(5分)
(2)设0<x1<x2,则
--(7分)
当0<x1<x2≤40时,x1-x2<0,1-
<0,得y1-y2>0,即 y1>y2.----------(9分)
当40<x1<x2时,x1-x2<0,1-
>0,得y1-y2<0,即 y1<y2.---(11分)
从而这个函数在(0,40]上是减函数,在[40,+∞)增函数,当x=40时,ymin=288000.
所以当池底是边长为40米的正方形时,总造价最低为288000元.---------------(14分)
| 1600 |
| x |
则池壁的面积为8(x+
| 1600 |
| x |
所以总造价:y=1600(x+
| 1600 |
| x |
(2)设0<x1<x2,则
|
当0<x1<x2≤40时,x1-x2<0,1-
| 1600 |
| x1x2 |
当40<x1<x2时,x1-x2<0,1-
| 1600 |
| x1x2 |
从而这个函数在(0,40]上是减函数,在[40,+∞)增函数,当x=40时,ymin=288000.
所以当池底是边长为40米的正方形时,总造价最低为288000元.---------------(14分)
点评:本题考查函数模型的构建,考查函数解析式的求解及常用方法,考查利用数学知识解决实际问题,属于基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 水是生命之源、生产之要、生态之基.2010年春季,西南5省面临世纪大旱,5000多万同胞受灾.这场少见的世纪大旱使农作物受灾面积近500万公顷,其中40万公顷良田颗粒无收,2000万同胞面临无水可饮的绝境.某乡镇对此次旱灾进行了认真的分析、总结,决定建造一个容积为4800m3,深为3m的长方体形无盖贮水池,以解决当地居民饮水、灌溉问题.已知贮水池池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底一边长为xm,总造价为y(单位:元).
水是生命之源、生产之要、生态之基.2010年春季,西南5省面临世纪大旱,5000多万同胞受灾.这场少见的世纪大旱使农作物受灾面积近500万公顷,其中40万公顷良田颗粒无收,2000万同胞面临无水可饮的绝境.某乡镇对此次旱灾进行了认真的分析、总结,决定建造一个容积为4800m3,深为3m的长方体形无盖贮水池,以解决当地居民饮水、灌溉问题.已知贮水池池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底一边长为xm,总造价为y(单位:元).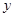 元表示为池底的一边长
元表示为池底的一边长 米的函数;
米的函数;