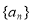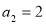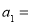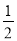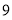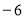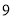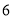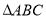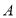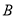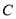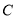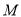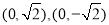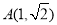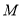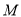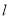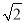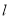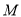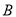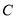题目内容
数列 的前
的前 项和为
项和为 ,
, ,
,
 .
.
(1)求 ;
;
(2)求数列 的通项
的通项 ;
;
(3)求数列 的前
的前 项和
项和 .
.
(1) ,
, ;(2)
;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)由 ,
, 分别算出
分别算出 即可;(2)由
即可;(2)由 ,再得到一个等式
,再得到一个等式 ,采用两式相减可得到
,采用两式相减可得到 ,再根据等比数列的通项公式写出
,再根据等比数列的通项公式写出 即可;(3)数列
即可;(3)数列 是由一个等差数列
是由一个等差数列 与一个等比数列
与一个等比数列 相乘得到,故它的前
相乘得到,故它的前 项和采用错位相减法进行求和即可.
项和采用错位相减法进行求和即可.
试题解析:(1) 1分
1分
 2分
2分
(2) ,
, ,
, 3分相减得
3分相减得
 4分,
4分,
即 5分
5分
对于 也满足上式 6分
也满足上式 6分
 数列
数列 是首项为2,公比为
是首项为2,公比为 的等比数列, 7分
的等比数列, 7分
 8分
8分
(3)
 9分
9分
 10分
10分
相减得, 11分
11分
 12分
12分
 13分
13分

 14分.
14分.
考点:1.等比数列的通项公式;2.数列的前 项和.
项和.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目