ЬтФПФкШн
0ЃМІСЃМ1,0ЃМІТЃМ1ЃЌЪ§Са{xn},{yn}гЩвдЯТЬѕМўШЗЖЈЃК(x1,y1)=(2,1),(xn+1,yn+1)=(ІСxn+1-ІС,ІТyn+2-2ІТ), (n=1,2,3,Ё)ЭъГЩвдЯТЮЪЬт.(1)ЧѓЪ§Са{xn}гы{yn}ЕФЭЈЯюЃЛ
(2)Чѓ![]() xnЃЌ
xnЃЌ![]() ynЃЛ
ynЃЛ
(3)Ъ§Са{xn},{yn}ЪЧгаЯоЪ§СаЪБЃЌЕБІС=ІТЪБЃЌЧѓЕу(xn,yn)ЕФДцдкЗЖЮЇЃЛ
(4)Ъ§Са{xn},{yn}ЪЧгаЯоЪ§СаЪБЃЌЕБІТЁнІС2ЪБЃЌНЋЕу(xn,yn)ЕФДцдкЗЖЮЇгУЭМаЮБэЪОГіРД.
НтЃК(1)гЩЬтЩшЕУ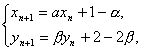 Ёр
Ёр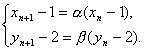
Ёр{xn-1}гы{yn-2}ЪЧЙЋБШЗжБ№ЮЊІС,ІТЕФЕШБШЪ§Са.
Ёр гж
гж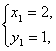
Ёр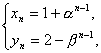 n=1ЪБвВГЩСЂ.
n=1ЪБвВГЩСЂ.
(2)Ёп0ЃМІСЃМ1,0ЃМІТЃМ1,Ёр![]() xn=1,
xn=1,![]() yn=2.
yn=2.
(3)(x1,y1)=(2,1),2ЁмkЁмnЪБЃЌгЩІС=ІТ,xk=1+ІСk-1,yk=2-ІСk-1.
ЯћШЅІСk-1ЕУxk+yk=3,гЩkЁн2МА0ЃМІСЃМ1,
ЁрЕу(xn,yn)дкЯпЖЮx+y=3(1ЃМxЁм2)ЩЯ.

(4)(x1,y1)=(2,1),2ЁмkЁмnЪБ,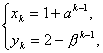 k-1ЃО0,
k-1ЃО0,
гЩ(2)ЕУ1ЃМxkЃМ2,1ЃМykЃМ2,гж(ІСk-1)2=(xk-1)2,
Ёр(ІС2)k-1=(xk-1)2.ЁпІТЁнІС2,ЁрІТk-1Ён(ІС2)k-1,МД2-ykЁн(xk-1)2.
ЁрykЁм-(xk-1)2+2,ЁрЕу(xn,yn)ЫљдкЕФЗЖЮЇЪЧyЁм-(x-1)2+2Чв1ЃМxЃМ2,1ЃМyЃМ2МАЕу(2ЃЌ1)ЃЌЦфЭМаЮЮЊЭМжавѕгАВПЗж.

 бєЙтЭЌбЇвЛЯпУћЪІШЋгХКУОэЯЕСаД№АИ
бєЙтЭЌбЇвЛЯпУћЪІШЋгХКУОэЯЕСаД№АИдкФГаЃОйааЕФЪ§бЇОКШќжаЃЌШЋЬхВЮШќбЇЩњЕФОКШќГЩМЈНќЫЦЗўДге§ЬЌЗжВМ![]() ЁЃвбжЊГЩМЈдк90ЗжвдЩЯЃЈКЌ90ЗжЃЉЕФбЇЩњга12УћЁЃ
ЁЃвбжЊГЩМЈдк90ЗжвдЩЯЃЈКЌ90ЗжЃЉЕФбЇЩњга12УћЁЃ
ЃЈЂёЃЉЁЂЪдЮЪДЫДЮВЮШќбЇЩњзмЪ§дМЮЊЖрЩйШЫЃП
ЃЈЂђЃЉЁЂШєИУаЃМЦЛЎНБРјОКШќГЩМЈХХдкЧА50УћЕФбЇЩњЃЌЪдЮЪЩшНБЕФЗжЪ§ЯпдМЮЊЖрЩйЗжЃП
ПЩЙВВщдФЕФЃЈВПЗжЃЉБъзМе§ЬЌЗжВМБэ![]()
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.2 1.3 1.4 1.9 2.0 2.1 | 0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 | 0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 | 0.888 0.9066 0.9222 0.9726 0.9783 0.9830 | 0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 | 0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 | 0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 | 0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 | 0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 | 0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 | 0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
ЕуЦРЃКБОаЁЬтжївЊПМВще§ЬЌЗжВМЃЌЖдЖРСЂЪТМўЕФИХФюКЭБъзМе§ЬЌЗжВМЕФВщдФЃЌПМВщдЫгУИХТЪЭГМЦжЊЪЖНтОіЪЕМЪЮЪЬтЕФФмСІЁЃ
дкФГаЃОйааЕФЪ§бЇОКШќжаЃЌШЋЬхВЮШќбЇЩњЕФОКШќГЩМЈНќЫЦЗўДге§ЬЌЗжВМ![]() ЁЃвбжЊГЩМЈдк90ЗжвдЩЯЃЈКЌ90ЗжЃЉЕФбЇЩњга12УћЁЃ
ЁЃвбжЊГЩМЈдк90ЗжвдЩЯЃЈКЌ90ЗжЃЉЕФбЇЩњга12УћЁЃ
ЃЈЂёЃЉЁЂЪдЮЪДЫДЮВЮШќбЇЩњзмЪ§дМЮЊЖрЩйШЫЃП
ЃЈЂђЃЉЁЂШєИУаЃМЦЛЎНБРјОКШќГЩМЈХХдкЧА50УћЕФбЇЩњЃЌЪдЮЪЩшНБЕФЗжЪ§ЯпдМЮЊЖрЩйЗжЃП
ПЩЙВВщдФЕФЃЈВПЗжЃЉБъзМе§ЬЌЗжВМБэ![]()
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.2 1.3 1.4 1.9 2.0 2.1 | 0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 | 0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 | 0.888 0.9066 0.9222 0.9726 0.9783 0.9830 | 0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 | 0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 | 0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 | 0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 | 0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 | 0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 | 0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |