Question

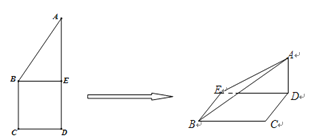
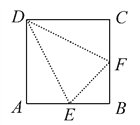
【题目】如图，在边长为2a的正方形ABCD中，E，F分别为AB，BC的中点，沿图中虚线将3个三角形折起，使点A，B，C重合，重合后记为点P.

问：(1)折起后形成的几何体是什么几何体？

(2)这个几何体共有几个面，每个面的三角形有何特点？

(3)每个面的三角形面积为多少？

Answer 1

【答案】（1）三棱锥；（2）见解析；（3）见解析

【解析】试题分析：（1）棱锥侧面为三角形，几棱锥决定于底面边数（2）三个侧面加上一个底面，都是直角三角形（3）根据直角情况，分别求对应直角边，再根据直角三角形面积公式求各自面积

试题解析：(1)如图，折起后的几何体是三棱锥.

(2)这个几何体共有4个面，其中△DEF为等腰三角形，△PEF为等腰直角三角形，△DPE和△DPF均为直角三角形.

(3)S△PEF=a2，S△DPF=S△DPE=×2a×a=a2，

S△DEF=S正方形ABCD-S△PEF-S△DPF-S△DPE=(2a)2-a2-a2-a2=a2.