题目内容
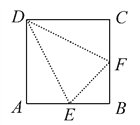
【题目】如图正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
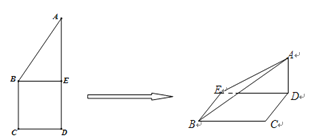
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:
点,则翻折后的几何体中有如下描述:
①![]() 与
与![]() 所成角的正切值是
所成角的正切值是![]() ;
;
②![]() ∥
∥![]() ;
;
③![]() 的体积是
的体积是![]() ;
;
④平面![]() ⊥平面
⊥平面![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
其中正确的有 .(填写你认为正确的序号)
【答案】①④⑤
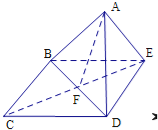
【解析】试题分析:①由于BC∥DE,则∠ABC(或其补角)为AB与DE所成角;
②AB和CE是异面直线;
③根据三棱锥的体积公式即可求VB﹣ACE的体积;
④根据面面垂直的判定定理即可证明;
⑤根据直线和平面所成角的定义进行求解即可.
解:由题意,AB=![]() BC,AE=
BC,AE=![]() a,
a,
AD⊥平面BCDE,AD=a,AC=![]() a
a
①由于BC∥DE,∴∠ABC(或其补角)为AB与DE所成角
∵AB=![]() a,BC=a,AC=
a,BC=a,AC=![]() a,
a,
∴BC⊥AC,∴tan∠ABC=![]() ,故①正确;
,故①正确;
②由图象可知AB与CE是异面直线,故②错误.
③VB﹣ACE的体积是![]() S△BCE×AD=
S△BCE×AD=![]() ×
×![]() a3=
a3=![]() ,故③正确;
,故③正确;
(4)∵AD⊥平面BCDE,BC平面BCDE,
∴AD⊥BC,∵BC⊥CD,AD∩CD=D,∴BC⊥平面ADC,
∵BC平面ABC,∴平面ABC⊥平面ADC,故④正确;
⑤连接CE交BD于F,则EF⊥BD,
∵平面ABD⊥平面BDE,
∴EF⊥平面ABD,连接F,
则∠EAF为直线AE与平面ABD所成角,
在△AFE中,EF=![]() ,AE=
,AE=![]() a,
a,
∴sin∠EAF=![]() =
=![]() ,则∠EAF=30°,故⑤正确,
,则∠EAF=30°,故⑤正确,
故正确的是①③④⑤
故答案为:①③④⑤

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目