题目内容
已知函数f（θ）=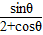
，则 f′（0）= ．
【答案】分析：利用求导法则得到导函数，将导函数x=0代入求出函数值即可．
解答：解：函数f（θ）=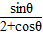
，
则 f′（θ）=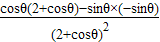
=
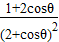
所以f′（0）=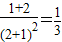
故答案为
点评：本题考查三角函数及除法求导法则，属于基础题．
解答：解：函数f（θ）=
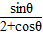，则 f′（θ）=
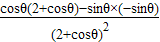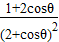
=所以f′（0）=
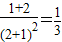
故答案为
点评：本题考查三角函数及除法求导法则，属于基础题．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
已知函数f（x）=alnx+x2 （a为实常数），e为自然对数的底数．
（1）求函数f（x）在[1，e]上的最小值；
（2）若存在x∈[1，e]，使得不等式f（x）≤（a+2）x成立，求实数a的取值范围．
（1）求函数f（x）在[1，e]上的最小值；
（2）若存在x∈[1，e]，使得不等式f（x）≤（a+2）x成立，求实数a的取值范围．
3、已知函数f（x）=ax3+bx2+cx+d的图象如图，则（ ）已知函数f（x）满足：x≥4，则f（x）=(
)x；当x＜4时f（x）=f（x+1），则f（2+log23）=（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|