题目内容
对于函数f(x),若在其定义域内存在两个实数a,b(a<b),使当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“布林函数”,区间[a,b]称为函数f(x)的“等域区间”.
(1)布林函数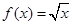 的等域区间是 .
的等域区间是 .
(2)若函数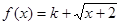 是布林函数,则实数k的取值范围是 .
是布林函数,则实数k的取值范围是 .
(1)[0,1];(2) .
.
解析试题分析:(1)因为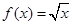 是增函数,则当x∈[a,b]时,f(x)∈[f(a),f(b)].
是增函数,则当x∈[a,b]时,f(x)∈[f(a),f(b)].
令f(a)=a,且f(b)=b,即 ,且
,且 ,则a=0,b=1.
,则a=0,b=1.
故布林函数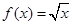 的等域区间是[0,1].
的等域区间是[0,1].
(2)
因为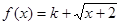 是增函数,若
是增函数,若 是布林函数,则
是布林函数,则
存在实数a,b(-2≤a<b),使 ,即
,即 .所以a,b为方程
.所以a,b为方程 的两个实数根,从而方程
的两个实数根,从而方程 有两个不等实根.
有两个不等实根.
令 ,则
,则 .当
.当 时,
时, ;当
;当 时,
时, .
.
由图可知,当 时,直线
时,直线 与曲线
与曲线 有两个不同交点,即方程
有两个不同交点,即方程 有两个不等实根,故实数k的取值范围是
有两个不等实根,故实数k的取值范围是 .
.
考点:新概念的理解、方程的根与函数的图像

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 的值域是 .
的值域是 . 的零点个数是 .
的零点个数是 . 在
在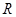 上有两个零点,则实数
上有两个零点,则实数 的取值范围是________.
的取值范围是________. 是函数
是函数 且
且 的反函数,且函数
的反函数,且函数 , 则
, 则 ____________.
____________. 的值域为
的值域为 ,则
,则 的取值范围是 .
的取值范围是 . 的方程
的方程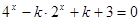 只有一个实数解,则实数
只有一个实数解,则实数 的取值范围是_______.
的取值范围是_______. 、
、 为正实数,函数
为正实数,函数 在
在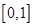 上的最大值为
上的最大值为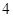 ,则
,则 在
在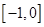 上的最小值为 .
上的最小值为 .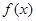 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,则
,则 ________
________ (用“>”或“<”填空).
(用“>”或“<”填空).