题目内容
利用基本不等式求 的最值?当0<x<1时,如何求
的最值?当0<x<1时,如何求 的最大值.
的最大值.
解:(1)当=0时,y=0,
当x≠0时, =
= ,
,
用基本不等式
若x>0时,0<y≤ ,
,
若x<0时,- ≤y<0,
≤y<0,
综上得,可以得出- ≤y≤
≤y≤ ,
,
∴ 的最值是-
的最值是- 与
与 .
.
(2) =
=
∵0<x<1
∴1<x+1<2
∴ =
= ≤
≤
等号当且仅当x= 成立.
成立.
综上, 的最值是-
的最值是- 与
与 .当0<x<1时,
.当0<x<1时, 的最大值是
的最大值是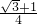 .
.
分析:将 ,当x=0时,y=0,当x≠0时,
,当x=0时,y=0,当x≠0时, =
= ,当x>0时,0<y≤
,当x>0时,0<y≤ ,当x<0时,-
,当x<0时,- ≤y<0,可以得出-
≤y<0,可以得出- ≤y≤
≤y≤ ,得出最值即可,同理对
,得出最值即可,同理对 进行变行求最值.
进行变行求最值.
点评:本题通过构造形式用基本不等式求最值,训练答题都观察、化归的能力.
当x≠0时,
 =
= ,
,用基本不等式
若x>0时,0<y≤
 ,
,若x<0时,-
 ≤y<0,
≤y<0,综上得,可以得出-
 ≤y≤
≤y≤ ,
,∴
 的最值是-
的最值是- 与
与 .
.(2)
 =
=
∵0<x<1
∴1<x+1<2
∴
 =
= ≤
≤
等号当且仅当x=
 成立.
成立.综上,
 的最值是-
的最值是- 与
与 .当0<x<1时,
.当0<x<1时, 的最大值是
的最大值是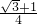 .
.分析:将
 ,当x=0时,y=0,当x≠0时,
,当x=0时,y=0,当x≠0时, =
= ,当x>0时,0<y≤
,当x>0时,0<y≤ ,当x<0时,-
,当x<0时,- ≤y<0,可以得出-
≤y<0,可以得出- ≤y≤
≤y≤ ,得出最值即可,同理对
,得出最值即可,同理对 进行变行求最值.
进行变行求最值.点评:本题通过构造形式用基本不等式求最值,训练答题都观察、化归的能力.

练习册系列答案
相关题目
 的最值?当0<x<1时,如何求
的最值?当0<x<1时,如何求 的最大值.
的最大值.