题目内容
设p:方程x2+y2+kx+ky+k2-2=0表示圆;q:函数f(x)=(k-1)x+1在R上是增函数.如果p∨q是真命题,p∧q是假命题,求实数k的取值范围.
分析:对方程配方,可得命题p为真时的条件;根据一次函数为增函数可得命题q为真时的条件.根据复合命题真值表,可得p与q,一真一假,由此可得k的范围.
解答:解:方程x2+y2+kx+ky+k2-2=0⇒(x+
)2+(y+
)2=2-
,
方程表示圆,则2-
>0⇒k2<4⇒-2<k<2,
∴命题p为真时:-2<k<2,
由函数f(x)=(k-1)x+1在R上是增函数.得:k>1,
∴命题q为真时:k>1,
若p∨q是真命题,p∧q是假命题,由复合命题真值表得:p与q,一真一假.
若p真q假,则有
⇒-2<k≤1;
若p假q真,则有
⇒k≥2.
综上所述,实数k的取值范围是-2<k≤1或k≥2.
| k |
| 2 |
| k |
| 2 |
| k2 |
| 2 |
方程表示圆,则2-
| k2 |
| 2 |
∴命题p为真时:-2<k<2,
由函数f(x)=(k-1)x+1在R上是增函数.得:k>1,
∴命题q为真时:k>1,
若p∨q是真命题,p∧q是假命题,由复合命题真值表得:p与q,一真一假.
若p真q假,则有
|
若p假q真,则有
|
综上所述,实数k的取值范围是-2<k≤1或k≥2.
点评:本题借助考查复合命题的真假判断,考查了圆的标准方程与一次函数的单调性,要熟练掌握复合命题真值表.

练习册系列答案
相关题目
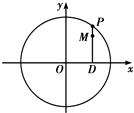 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的射影,M为PD上一点,且|MD|=
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的射影,M为PD上一点,且|MD|=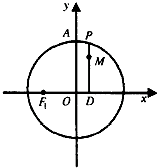 如图,设P是圆x2+y2=2上的动点,PD⊥x轴,垂足为D,M为线段PD上一点,且|PD|=
如图,设P是圆x2+y2=2上的动点,PD⊥x轴,垂足为D,M为线段PD上一点,且|PD|= (2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且
(2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且