题目内容
关于x的方程x3-3x2-a=0有三个不同的实数解,求a的取值范围.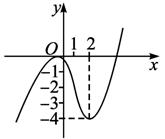
分析:本题是高次方程,直接去研究难度大,故可转化为y=x3-3x2与直线y=a的交点讨论.
解:由x3-3x2-a=0,得a=x3-3x2.令y=x3-3x2,y′=3x2-6x=3x(x-2).
由y′=0得x=0或x=2.
当x∈(-∞,0)时,y′>0;
x∈(0,2)时,y′<0;
x∈(2,+∞)时,y′>0.
∴y在(-∞,0),(2,+∞)上递增,在(0,2)上递减.
∴当-4<a<0时,方程有三个不同实数解.

练习册系列答案
相关题目