题目内容
5、已知2002年4月20日是星期五,那么1090天后的今天是星期
六
.分析:将1090用底数含7的二项式表示,利用二项式定理展开,再将390用与7有关的二项式表示,利用二项式定理展开即得到1090被7除的余数.
解答:解:∵1090=(7+3)90=C900790+C90178931+…+C90897389+C9090390
又∵390=2730=(28-1)30=C3002830-C3012829+…-C302928+C3030
∴1090被7除余1
1090天后的今天是星期六
故答案为六
又∵390=2730=(28-1)30=C3002830-C3012829+…-C302928+C3030
∴1090被7除余1
1090天后的今天是星期六
故答案为六
点评:本题考查等价转换的能力及利用二项式定理解决整除性问题.

练习册系列答案
相关题目
 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小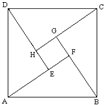 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小 .记直角三角形中的一个锐角为θ.
.记直角三角形中的一个锐角为θ.