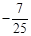题目内容
 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形.已知大正方形的面积是1,小正方形的面积是
| 1 | 25 |
(1)请根据本题题意写出sinθ与cosθ之间的等量关系,并求tanθ的值;
(2)解关于x的不等式logtanθ(x2-1)≥0.
分析:(1)根据大正方形的面积是1,小正方形的面积是
,可探求sinθ与cosθ之间的等量关系,从而求tanθ的值;
(2)根据tanθ的值,进行分类讨论,从而将不等式化为一元二次不等式,故可解.
| 1 |
| 25 |
(2)根据tanθ的值,进行分类讨论,从而将不等式化为一元二次不等式,故可解.
解答: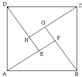 解:(1)如图,由已知设∠ABF=θ,易得:
解:(1)如图,由已知设∠ABF=θ,易得:
AB=1,EF=
,且AF=sinθ,BF=cosθ⇒|sinθ-cosθ|=
--------------------(3分)⇒sin2θ=
=
⇒12tan2θ-25tanθ+12=0,⇒tanθ=
或tanθ=
,
所以较大锐角正切值为
,且较小锐角的正切值为
--------------------------(3分)
(2)①当tanθ=
时,logtanθ(x2-1)≥0⇒x2-1≥1 ⇒x≤-
或x≥
②当tanθ=
时,logtanθ(x2-1)≥0⇒
⇒-
≤x<-1或1<x≤
---(6分)
 解:(1)如图,由已知设∠ABF=θ,易得:
解:(1)如图,由已知设∠ABF=θ,易得:AB=1,EF=
| 1 |
| 5 |
| 1 |
| 5 |
| 24 |
| 25 |
| 2tanθ |
| 1+tan2θ |
| 4 |
| 3 |
| 3 |
| 4 |
所以较大锐角正切值为
| 4 |
| 3 |
| 3 |
| 4 |
(2)①当tanθ=
| 4 |
| 3 |
| 2 |
| 2 |
②当tanθ=
| 3 |
| 4 |
|
| 2 |
| 2 |
点评:本题以实际问题为载体,考查三角函数,考查解不等式,关键是将实际问题转化为数学问题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
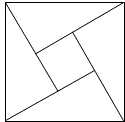 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是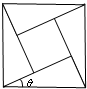 2002年8月,在北京召开国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形、与中间的小正方形拼成的大正方形.若直角三角形中较小的锐角为θ,大正方形的面积为1,小正方形的面积为
2002年8月,在北京召开国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形、与中间的小正方形拼成的大正方形.若直角三角形中较小的锐角为θ,大正方形的面积为1,小正方形的面积为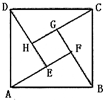 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较大的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较大的锐角为θ,大正方形的面积是1,小正方形的面积是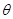 ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是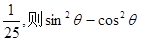 的值等于( )
的值等于( )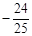 C.
C.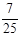 D.
D.